This is the twelfth part of the ILP series. For your convenience you can find other parts in the table of contents in Part 1 – Boolean algebra

In Part 3 we saw how to calculate exponentiation with constant exponent. Today we are going to implement the same operation, however, this time exponent will be a variable. Let’s begin.

Table of Contents

Introduction

First, let’s reiterate some assumptions we made during this course. We assumed that every variable has value not greater than $k = 2^n - 1, k, n \in \mathbb{N_+}$ . We introduced this constraint in Part 2 – Multiplication in order to be able to decompose the value using binary representation. However, we didn’t assume that the result of multiplication still hold this constraint — it could be much greater than $k$ . Of course we would not be able to utilize this option if we would try to multiply the result again.
We could do the same with exponentiation, e.g., assume that operands are not greater than $k$ , but the result is. This is a great idea, however, we are probably not able to perform calculations on such a big values because of floating point representation. Imagine that we want to calculate $2^{10000}$ — the result is so big that we will not be able to perform further calculations.
That is why we will make an assumption that the result is not greater than $k$ . This will simplify the problem and also allow us to implement really fast algorithm.

Test cases

Let’s assume that $n = 10$ which implies $k=1023$ . Using variables $a, b \in \mathbb{N}, a, b \le k$ we would like our operation to fulfill the following requirements:

$\begin{tabular}{|c|c|c|c|} \hline Test & a & b & a^b \\ \hline 1 & 0 & 0 & 1\\ 2 & 1 & 0 & 1\\ 3 & 2 & 0 & 1\\ 4 & 3 & 0 & 1\\ 5 & 1023 & 0 & 1\\ 6 & 0 & 1 & 0\\ 7 & 1 & 1 & 1\\ 8 & 2 & 1 & 2\\ 9 & 3 & 1 & 3\\ 10 & 1023 & 1 & 1023\\ 11 & 0 & 1023 & 0\\ 12 & 1 & 1023 & 1\\ 13 & 2 & 9 & 512\\ 14 & 3 & 5 & 729\\ 15 & 10 & 3 & 1000\\ \hline \end{tabular}$

In other words: every variable raised to the power of zero should be equal to one. Notice that we define $0^0$ as one because we cannot throw exception or ignore these values, what’s more, everyone does that. We want every value raised to the power of one be equal to the value itself, even very big value (as big as $k$ ). We also want to be able to calculate every exponentiation for which result is not greater than $k$ (so we want to be able to calculate $1023^1$ and $2^9$ ).

Corner cases

Let’s start with corner cases. Assuming that $x$ is our result, we have:

$a^b = x = b \stackrel{?}{=} 0\ ?\ 1\ :\ b \stackrel{?}{=} 1\ ?\ a\ :\ a \stackrel{?}{\le} 1\ ?\ a\ :\ y$

We have the following cases:

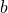$b$ is zero then we return one — because every value (even 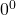$0^0$ ) raised to the power of zero is equal to one (tests 1-5)
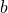$b$ is one then we return $a$ — because very value raised to the power of one is equal to the value itself (tests 6-10)
$a$ is not greater than one then we return $a$ — because one raised to any power is still equal to one (tests 11-12)

We also introduced $y$ which represents the ”casual” case — the case which needs actual exponentiation (tests 13-15).

Exponentiation by squaring

We will not avoid multiplication. We know how to do fast multiplication but we still want to multiply as little as possible. We can notice that when calculating $a^{10}$ we don’t need to multiply nine times (e.g., $a \cdot a \cdot a \cdot a \cdot \ldots$ ) because $a^{10} = \left(a^{5}\right)^2 = \left(a^4 \cdot a\right)^2 = \left(\left(\left(a^2\right)^2\right)^2\right)\cdot a^2$ . Exponentiation by squaring is based on this idea and we will do the same.
We assumed that $n=10$ . This means that $b \le 1023$ so in binary representation it has at most $10$ digits. Because we assumed that the result is not greater than $k$ we can safely ignore six digits — why? There are only two values which result of raising to the power of ten (and greater) can be represented using ten digits: these are zero and one. Indeed, $2^{10} = 1024 > k$ . So there is no need in handling exponents greater than nine because we cannot represent the result anyway. And we can represent $9$ using exactly four digits (which is $1001$ ) and that is why we can ignore the rest of them.
This means that we need to represent $b$ using $\left\lceil \log_2 n \right\rceil$ binary digits.

First formula

We are ready to define $y$ . This time we will use pseudo-code to define the algorithm:

currentPower = a
result = 1
digits = representation of a (from right to left)
for i = 0..digits.length do
	if i &gt; 0 then currentPower = currentPower * currentPower
	result = result * max(1, currentPower * digits[i])

currentPower = a

result = 1

digits = representation of a (from right to left)

for i = 0..digits.length do

if i > 0 then currentPower = currentPower * currentPower

result = result * max(1, currentPower * digits[i])

With every loop iteration we calculate square of current power. Next, we multiply the result by the current power multiplied by the next digit or one. Let’s consider an example $2^5$ . We have $a=2$ and $b=5=0101$ . We have the following values:

Before entering the loop:
currentPower = 2
result = 1
digits = 0101

Iteration one:
i = 0, digits[0] = 1
i is not greater than 0 so we have currentPower = 2
result = result * max(1, 2 * 1) = result * 2 = 2

Iteration two
i = 1, digits[1] = 0
i is greater than 0 so we have currentPower = currentPower * currentPower = 4
result = result * max(1, 4 * 0) = result = 2

Iteration three:
i = 2, digits[2] = 1
i is greater than 0 so we have currentPower = currentPower * currentPower = 16
result = result * max(1, 16 * 1) = 32

Iteration four:
i = 3, digits[3] = 1
i is greater than 0 so we have currentPower = currentPower * currentPower = 256
result = result * max(1, 256 * 0) = 32

Before entering the loop:

currentPower = 2

result = 1

digits = 0101

Iteration one:

i = 0, digits[0] = 1

i is not greater than 0 so we have currentPower = 2

result = result * max(1, 2 * 1) = result * 2 = 2

Iteration two

i = 1, digits[1] = 0

i is greater than 0 so we have currentPower = currentPower * currentPower = 4

result = result * max(1, 4 * 0) = result = 2

Iteration three:

i = 2, digits[2] = 1

i is greater than 0 so we have currentPower = currentPower * currentPower = 16

result = result * max(1, 16 * 1) = 32

Iteration four:

i = 3, digits[3] = 1

i is greater than 0 so we have currentPower = currentPower * currentPower = 256

result = result * max(1, 256 * 0) = 32

Looks great! But…
There is a problem with test 5. Observe that we calculate the square of the current power in every loop iteration. As we stated before it is not a problem because we don’t require the result of multiplication to be not greater than $k$ , so we can easily calculate $1023 \cdot 1023$ . But when we perform another loop iteration we need to represent the result of previous multiplication using exactly ten binary digits which is impossible!

But we handle corner cases!

You might think that there is no problem because we have already handled the corner cases. But this is not true. We need to remember that ILP is a declarative paradigm and we need to represent every possible operation outcome. Yes, we use conditions to select correct value for edge case, but every operand is evaluated and we just cannot calculate the value for false branch.

Second formula

So how do we get rid of this problem? We can easily check whether we have to calculate edge case and make current power smaller:

currentPower = isThisCornerCase ? 1 : a
result = 1
digits = representation of a (from right to left)
for i = 0..digits.length do
	if i &gt; 0 then currentPower = currentPower * currentPower
	result = result * max(1, currentPower * digits[i])

currentPower = isThisCornerCase ? 1 : a

result = 1

digits = representation of a (from right to left)

for i = 0..digits.length do

if i > 0 then currentPower = currentPower * currentPower

result = result * max(1, currentPower * digits[i])

We have modified only one line (the first one) but now everything works great. For edge case $1023^1$ we raise one instead of $1023$ and everything should be great. However, there is a problem with test 15: $10^3$ . In every loop iteration we still calculate the square of the current power even if there are no more non-zero digits left. Let’s see this:

Before entering the loop:
currentPower = 10
result = 1
digits = 0011

Iteration one:
i = 0, digits[0] = 1
i is not greater than 0 so we have currentPower = 10
result = result * max(1, 10 * 1) = result * 10 = 10

Iteration two
i = 1, digits[1] = 1
i is greater than 0 so we have currentPower = currentPower * currentPower = 100
result = result * max(1, 100 * 1) = result = 1000

Iteration three:
i = 2, digits[2] = 0
i is greater than 0 so we have currentPower = currentPower * currentPower = 10000
result = result * max(1, 10000 * 0) = 1000

Iteration four:
i = 3, digits[3] = 0
i is greater than 0 so we have currentPower = currentPower * currentPower = 10000 * 10000 = 
	error! 
	we cannot represent 10000 using 10 digits and we cannot perform multiplication

Before entering the loop:

currentPower = 10

result = 1

digits = 0011

Iteration one:

i = 0, digits[0] = 1

i is not greater than 0 so we have currentPower = 10

result = result * max(1, 10 * 1) = result * 10 = 10

Iteration two

i = 1, digits[1] = 1

i is greater than 0 so we have currentPower = currentPower * currentPower = 100

result = result * max(1, 100 * 1) = result = 1000

Iteration three:

i = 2, digits[2] = 0

i is greater than 0 so we have currentPower = currentPower * currentPower = 10000

result = result * max(1, 10000 * 0) = 1000

Iteration four:

i = 3, digits[3] = 0

i is greater than 0 so we have currentPower = currentPower * currentPower = 10000 * 10000 =

error!

we cannot represent 10000 using 10 digits and we cannot perform multiplication

So how do solve this problem? In every loop iteration we can check whether it makes sense to calculate next square. If there are no more non-zero digits than we can stop squaring the current power (but we need to continue loop – we are declaring results, not calculating them on the fly!). So we get:

currentPower = isThisCornerCase ? 1 : a
result = 1
digits = representation of a (from right to left)
for i = 0..digits.length do
	if i &gt; 0 then
		currentPower = min(currentPower, thereAreNonZeroDigitsLeft * k)
		currentPower = currentPower * currentPower
	result = result * max(1, currentPower * digits[i])

currentPower = isThisCornerCase ? 1 : a

result = 1

digits = representation of a (from right to left)

for i = 0..digits.length do

if i > 0 then

currentPower = min(currentPower, thereAreNonZeroDigitsLeft * k)

currentPower = currentPower * currentPower

result = result * max(1, currentPower * digits[i])

As you can see, when there are no more non-zero digits then currentPower is set to zero (because second argument of $\min$ function is equal to zero).

Summary

We are now able to calculate exponentiations with non-constant exponent. We are also able to calculate roots with non-constant degree using the same reasoning as for constant degree in Part 3. In the next part we will calculate factorial function. See you soon!