This is the thirtieth part of the ILP series. For your convenience you can find other parts in the table of contents in Part 1 – Boolean algebra
Today we are going to implement something simple — Factorial function. We will use tricks similar to the ones used in previous part.
Introduction
Factorial function is defined naturally for all non-negative integers. Basically, it is a product of all positive integers less than or equal to the argument of the function. Additionally, the factorial of zero is defined as one. We will define exactly the same using the following variables:
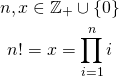
If you try to calculate this function for some small values you will notice that the factorial function rises really fast. For instance, ![]() . This means that it is no use in considering really big arguments because we will not be able to represent them using casual int32 representation. For our purposes we will assume that
. This means that it is no use in considering really big arguments because we will not be able to represent them using casual int32 representation. For our purposes we will assume that ![]() .
.
Actual formula
Since we know the upper bound for ![]() we can easily implement the formula:
we can easily implement the formula:
![Rendered by QuickLaTeX.com \[ x = \prod_{i=0}^{11} \max \left(1, n - i \right) \]](../../../../wp-content/ql-cache/quicklatex.com-d15e865cb93c36edfdc58f9eb069fcb9_l3.png)
This works in the following way: because ![]() , we need to multiply at most 12 numbers. In every loop iteration we subtract
, we need to multiply at most 12 numbers. In every loop iteration we subtract ![]() from
from ![]() and take the maximum of the difference and one. We do that because we don’t know the value of
and take the maximum of the difference and one. We do that because we don’t know the value of ![]() and we cannot allow the result to be zeroed. Take a look at this example:
and we cannot allow the result to be zeroed. Take a look at this example:
![]()
For every ![]() greater or equal to
greater or equal to ![]() the maximum function returns
the maximum function returns ![]() so we can be sure that the result is not zeroed. What’s more, we have
so we can be sure that the result is not zeroed. What’s more, we have ![]() as we wanted before.
as we wanted before.
Summary
So far we have been using ILP to implement various operations using declarative approach. We have seen that even though ILP uses only trivial tools we are able to implement some fancy functions. We have also seen how to implement strictly imperative construct (if). In the next part we are going to implement another thing from imperative world: loop. Stay tuned.