This is the sixth part of the ILP series. For your convenience you can find other parts in the table of contents in Part 1 – Boolean algebra
Last time we saw how to define minimum in ILP. We also know how to multiply variables using long multiplication algorithm. Our algorithms work, however, they are slow. Today we are going to utilize ![]() function to speed up multiplication.
function to speed up multiplication.
Table of Contents
General idea
We know how to multiply variables. Basically, we decompose both arguments and extract digits. Next, we multiply every pair of digits using conjuction, and multiply the result by power of two (which is constant).
As we said in part 2, this requires ![]() temporary variables because we need to store every conjunction in some temporary variable. However, when we perform long multiplication on a piece of paper we do not multiply every two digits but we multiply digit
temporary variables because we need to store every conjunction in some temporary variable. However, when we perform long multiplication on a piece of paper we do not multiply every two digits but we multiply digit ![]() by whole argument
by whole argument ![]() (using notation from part 2). We can do the same in ILP.
(using notation from part 2). We can do the same in ILP.
Improvement
We know that we cannot multiply variables just like that because we need to use only linear constraints so once again we are going to use some trick. We have the following variables:
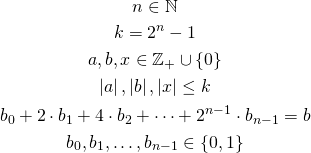
We have arguments (![]() ), result (
), result (![]() ), decomposition (
), decomposition (![]() ), and the maximum possible value (
), and the maximum possible value (![]() ). Now we are going to multiply every digit
). Now we are going to multiply every digit ![]() by argument
by argument ![]() using
using ![]() function.
function.
Let’s consider the value of ![]() . When
. When ![]() is zero then the whole value is zero (because it is
is zero then the whole value is zero (because it is ![]() ). When
). When ![]() is one the result is equal to
is one the result is equal to ![]() . We also know that
. We also know that ![]() which implies
which implies ![]() . This is in fact equivalent to
. This is in fact equivalent to ![]() . When
. When ![]() is zero we get
is zero we get ![]() . When
. When ![]() is one we obtain
is one we obtain ![]() and because
and because ![]() we get
we get ![]() . We also need to remember that
. We also need to remember that ![]() is a constant value so we are allowed to calculate
is a constant value so we are allowed to calculate ![]() .
.
Final formula
Now we can define the final formula:
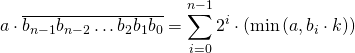
We simply multiply every digit by ![]() and then by the power of two.
and then by the power of two.
Summary
We are now able to calculate multiplication using only ![]() temporary variables which is a great improvement. In the next part we are going to see how to multiply negative values using today’s algorithm and absolute value function defined in previous part.
temporary variables which is a great improvement. In the next part we are going to see how to multiply negative values using today’s algorithm and absolute value function defined in previous part.