This is the fifty ninth part of the ILP series. For your convenience you can find other parts in the table of contents in Part 1 – Boolean algebra
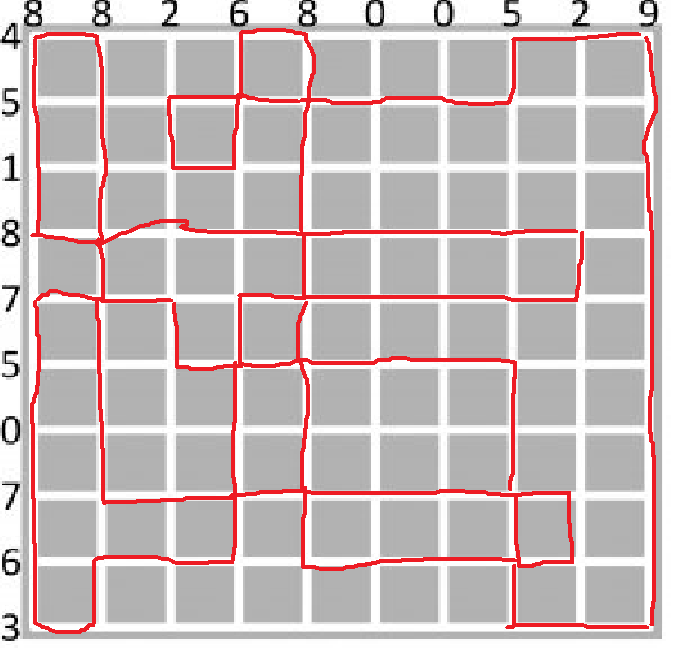
Today we are going to solve Pętliczek. We have a chessboard of any size. Each column and row has a number associated which indicates how many edges in that line can be used. We need to build a continuous path (a loop) meeting the criteria. The line can self cross.
The code:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 |
var solver = new CplexMilpSolver(23); var columns = new int []{8,8,2,6,8,0,0, 5,2,9}; var rows = new int[] {4,5,1,8,7,5,0,7,6,3}; var width = columns.Length; var height = rows.Length; Console.WriteLine("Create variables"); var edges = new List<List<System.Dynamic.ExpandoObject>>(); for(var row = 0; row < height;++row){ var rowVars = new List<System.Dynamic.ExpandoObject>(); for(var column = 0; column < width;++column){ dynamic expando = new System.Dynamic.ExpandoObject(); if(column < width - 1){ expando.Right = solver.CreateAnonymous(Domain.BinaryInteger); } if(row < height - 1){ expando.Bottom = solver.CreateAnonymous(Domain.BinaryInteger); } expando.IdVar = solver.CreateAnonymous(Domain.PositiveOrZeroInteger); rowVars.Add(expando); } edges.Add(rowVars); } Console.WriteLine("Set edges in columns"); for(var column = 0; column < width;++column){ var columnVars = Enumerable.Range(0, height - 1).Select(i => edges[i][column]).ToArray(); var toAdd = new List<IVariable>(); foreach(dynamic expando in columnVars){ toAdd.Add(expando.Bottom); } solver.Set(ConstraintType.Equal, solver.Operation(OperationType.Addition, toAdd.ToArray()), solver.FromConstant(columns[column])); } Console.WriteLine("Set edges in rows"); for(var row = 0; row < height;++row){ var rowVars = Enumerable.Range(0, width - 1).Select(i => edges[row][i]).ToArray(); var toAdd = new List<IVariable>(); foreach(dynamic expando in rowVars){ toAdd.Add(expando.Right); } solver.Set(ConstraintType.Equal, solver.Operation(OperationType.Addition, toAdd.ToArray()), solver.FromConstant(rows[row])); } Console.WriteLine("Make sure line is continuous"); for(var row = 0; row < height;++row){ for(var column = 0; column < width;++column){ dynamic self = edges[row][column]; var neighbours = new List<IVariable>(); if(row > 0){ dynamic up = edges[row-1][column]; neighbours.Add(up.Bottom); } if(row < height - 1){ dynamic down = edges[row+1][column]; neighbours.Add(self.Bottom); } if(column > 0){ dynamic left = edges[row][column-1]; neighbours.Add(left.Right); } if(column < width - 1){ dynamic right = edges[row][column+1]; neighbours.Add(self.Right); } var sum = solver.Operation(OperationType.Addition, neighbours.ToArray()); var empty = solver.Operation(OperationType.IsEqual, sum, solver.FromConstant(0)); var connection = solver.Operation(OperationType.IsEqual, sum, solver.FromConstant(2)); var cross = solver.Operation(OperationType.IsEqual, sum, solver.FromConstant(4)); solver.Set(ConstraintType.Equal, solver.Operation(OperationType.Disjunction, empty, connection, cross), solver.FromConstant(1)); } } Console.WriteLine("Make sure there is one line"); var goal = solver.FromConstant(0); solver.AddGoal("Goal", goal.Operation(OperationType.Negation)); solver.Solve(); for(var row = 0; row < height;++row){ for(var column = 0; column < width - 1; ++ column){ dynamic self = edges[row][column]; Console.Write(solver.GetValue(self.Right) > 0 ? " -" : " "); } Console.WriteLine(); if(row < height - 1){ for(var column = 0; column < width; ++ column){ dynamic self = edges[row][column]; Console.Write(solver.GetValue(self.Bottom) > 0 ? "| " : " "); } } Console.WriteLine(); } |
In lines 3 and 4 we define the board.
Lines 9-30 create variables. For each column and row crossing point we create three variables: one for edge going right, one for edge going down, one for the loop (we’ll come to that later).
In lines 32-41 we make sure we meet the constraint for columns. Similarly in lines 43-51 for rows.
Now we need to make sure the line is continuous. Similarly to the approach from the last part, each crossing point can have zero edges, two edges (for a straight line or a turning) or four edges (for self crossing). So we take edges from the point and from neighbors and then do some math.
Once again, we don’t make sure there is exactly one line because it just works. We’ll takle that challenge next time.
Output:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
Tried aggregator 2 times. MIP Presolve eliminated 2474 rows and 1634 columns. MIP Presolve modified 3331 coefficients. Aggregator did 246 substitutions. All rows and columns eliminated. Presolve time = 0.00 sec. (4.97 ticks) Root node processing (before b&c): Real time = 0.00 sec. (5.27 ticks) Parallel b&c, 4 threads: Real time = 0.00 sec. (0.00 ticks) Sync time (average) = 0.00 sec. Wait time (average) = 0.00 sec. ------------ Total (root+branch&cut) = 0.00 sec. (5.27 ticks) - - - - | | | | | | - - - - - | | | | | | - | | | | - - - - - - - - | | | | - - - - - - - | | | | | | - - - - - | | | | | | | | | | | | - - - - - - - | | | | | | - - - - - - | | | | - - - |
Printing the solution is interesting as well. Here in some more readable form: