This is the thirty fourth part of the ILP series. For your convenience you can find other parts in the table of contents in Part 1 – Boolean algebra
In the next part of ILP series we will implement Special ordered sets. These two constraints are pretty simple in their idea, Special ordered set of type 1 (SOS1) is used when we want to constraint that at most one of the variable has non-zero value. Special ordered set of type 2 (SOS2) adds two constraints: at most two variables can be non-zero, and if it is the case, these variables must be consecutive in their ordering. So set ![]() is SOS2, whereas set
is SOS2, whereas set ![]() is not (since non-zero variables do not stand next to each other).
is not (since non-zero variables do not stand next to each other).
Let’s begin with SOS1.
Special ordered set of type 1
We have the following variables:
![]()
For each index we create another binary variable:
![]()
We demand that at most one binary is non-zero:
![]()
And we specify constraint which will allow matching variable to take non-zero value:
![]()
Where ![]() is maximum integer value which our solver supports.
is maximum integer value which our solver supports.
How does it work? There can be at most one non-zero binary flag, and only for that flag the respective variable is allowed to take non-zero value (because for all the other flags constraint will have zero on both sides). However, non-zero flag does not require matching variable to be non-zero, but this does not break definition of SOS1.
Special ordered set of type 2
Now we want to add constraint that at most two variables are non-zero, and if there are two non-zero variables, they are next to each other. Using the same variables as before:
![]()
We create binary variables in the same way and still require that at most one binary is non-zero:
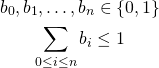
This time for each variable we take two binary flags into the constraint:
![]()
How does it work? Let’s assume that all ![]() are zeroes, this means that we have lots of constraints of the form
are zeroes, this means that we have lots of constraints of the form ![]() which makes sure that all
which makes sure that all ![]() are zeroes. However, imagine that
are zeroes. However, imagine that ![]() is true. This time we have two interesting constraints:
is true. This time we have two interesting constraints:
![]()
and
![]()
So ![]() and
and ![]() are allowed to be non-zero, so at most two variables can be non-zero.
are allowed to be non-zero, so at most two variables can be non-zero.
Summary
Special ordered sets looks easy but they are very useful. In next part we will see how to approximate any 1D or 2D function using SOS2.