This is the thirty fourth part of the ILP series. For your convenience you can find other parts in the table of contents in Part 1 – Boolean algebra

In the next part of ILP series we will implement Special ordered sets. These two constraints are pretty simple in their idea, Special ordered set of type 1 (SOS1) is used when we want to constraint that at most one of the variable has non-zero value. Special ordered set of type 2 (SOS2) adds two constraints: at most two variables can be non-zero, and if it is the case, these variables must be consecutive in their ordering. So set $[0,0,1,1,0]$ is SOS2, whereas set $[0,1,0,1,0]$ is not (since non-zero variables do not stand next to each other).

Let’s begin with SOS1.

Special ordered set of type 1

We have the following variables:

$\begin{gather*} a_0, a_1, \ldots, a_n \in \mathbb{R} \\ A = \{a_0, \ldots, a_n\} \end{gather*}$

For each index we create another binary variable:

$\begin{gather*} b_0, b_1, \ldots, b_n \in \{0, 1 \} \end{gather*}$

We demand that at most one binary is non-zero:

$\begin{gather*} \displaystyle\mathop{\sum}_{0 \le i \le n} b_i \le 1 \end{gather*}$

And we specify constraint which will allow matching variable to take non-zero value:

$\begin{gather*} \displaystyle\mathop{\forall}_{0 \le i \le n} -b_iK \le a_i \le b_iK \end{gather*}$

Where $K$ is maximum integer value which our solver supports.

How does it work? There can be at most one non-zero binary flag, and only for that flag the respective variable is allowed to take non-zero value (because for all the other flags constraint will have zero on both sides). However, non-zero flag does not require matching variable to be non-zero, but this does not break definition of SOS1.

Special ordered set of type 2

Now we want to add constraint that at most two variables are non-zero, and if there are two non-zero variables, they are next to each other. Using the same variables as before:

$\begin{gather*} a_0, a_1, \ldots, a_n \in \mathbb{R} \\ A = \{a_0, \ldots, a_n\} \end{gather*}$

We create binary variables in the same way and still require that at most one binary is non-zero:

$\begin{gather*} b_0, b_1, \ldots, b_n \in \{0, 1 \} \\ \displaystyle\mathop{\sum}_{0 \le i \le n} b_i \le 1 \end{gather*}$

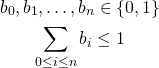
This time for each variable we take two binary flags into the constraint:

$\begin{gather*} \displaystyle\mathop{\forall}_{0 \le i \le n} -(b_i + b_{i+1}) K \le a_i \le (b_i + b_{i+1})K \end{gather*}$

How does it work? Let’s assume that all $b_{i}$ are zeroes, this means that we have lots of constraints of the form $-(0+0)K \le a_i \le (0+0)K$ which makes sure that all $a_i$ are zeroes. However, imagine that $b_i$ is true. This time we have two interesting constraints: