This is the thirty third part of the ILP series. For your convenience you can find other parts in the table of contents in Part 1 – Boolean algebra

Hi. Today we are going to implement lexicographical comparisons using ILP. Let’s begin!

Table of Contents

Introduction

Let’s assume that we want to solve the following:

$\begin{gather*} a_0, a_1, \ldots, a_n \in \mathbb{Z} \\ b_0, b_1, \ldots, b_n \in \mathbb{Z} \\ A = \{a_0, \ldots, a_n\}, B = \{b_0, \ldots, b_n\} \\ x = A \stackrel{?}{<} B\\ \end{gather*}$

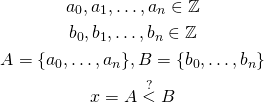
So we have two vectors of integer variables and we want to answer the question whether $A$ is less than $B$ . We define “less than” here in usual way, e.g., whether there exists $0 \le i \le n$ for which $\forall_{j=0}^{j-1} a_j = b_j$ and $a_i < b_i$ .

Naive implementation

We could implement this naively, e.g., perform all necessary comparisons and come up with the solution using conditions:

$\begin{gather*} x = (a_0 < b_0) \vee (a_0 = b_0 \wedge a_1 < b_1) \vee (a_0 = b_0 \wedge a_1 = b_1 \wedge a_2 < b_2) \vee \ldots \end{gather*}$

This is slow and inefficient. For $k$ elements in vector we have $k$ clauses and each clause contains up to $k$ conditions which sums up to $O(n^2)$ conditions. We can do better.

Better implementation using hashing

We can perform faster comparison using hashes. First, let’s assume that we can operate on numbers up to $2^{30}$ and that for now $n \le 29$ . We can do the following:

$\begin{gather*} y = (a_0 \stackrel{?}{>=} b_0 - a_0 \stackrel{?}{<=} b_0) \cdot 2^{n} + (a_1 \stackrel{?}{>=} b_1 - a_1 \stackrel{?}{<=} b_1) \cdot 2^{n-1} + (a_2 \stackrel{?}{>=} b_2 - a_2 \stackrel{?}{<=} b_2) \cdot 2^{n-2} + \ldots + (a_n \stackrel{?}{>=} b_n - a_n \stackrel{?}{<=} b_n) \cdot 2^{0} \\ x = y \stackrel{?}{<} 0 \end{gather*}$

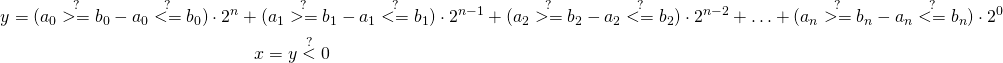
OK, some black magic. Let’s untangle it.

We compare each pair of vectors’ elements. For every pair we ask whether element from vector $A$ is greater or equal than element in vector $B$ and subtract flag whether it is less or equal. This results in extended binary solution (minus one or zero or one). Next, we multiply this binary flag by some constant power of two. We want to do it in a way which allows us to come out with final solution just by checking the sign of the sum.

Let’s see a simple example for the following data:

$\begin{gather*} A = \{ 5, 2, 4 \} \\ B = \{ 5, 4, 4 \} \\ y = (5 \stackrel{?}{>=} 5 - 5 \stackrel{?}{<=} 5)\cdot 2^{2} + (2 \stackrel{?}{>=} 4 - 2 \stackrel{?}{<=} 4)\cdot 2^{1} + \\ +(4 \stackrel{?}{>=} 4 - 4 \stackrel{?}{<=} 4)\cdot 2^{0} = (1-1) \cdot 4 + (0 - 1) \cdot 2 + (1 - 1) \cdot 1 = 0 - 2 + 0 = -2\\ x = y \stackrel{?}{<} 0 = 1 \end{gather*}$

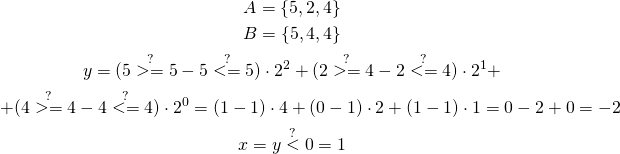
The idea here is: for every element we want to have positive positive term when element in vector $A$ is greater than element in vector $B$ , zero term when they are equal, and negative term when element in vector $A$ is less than element in vector $B$ . We achieve this by performing two comparisons: is greater or equal, and is less or equal. In the first case (element in $A$ is greater than element in $B$ ), we get $1 - 0 = 1$ . In second case we get $1 - 1 = 0$ , in third case we get $0 - 1 = -1$ .

Next, we want to get just one number representing the whole vector comparison. Since we compare numbers from left to right (see the definition of lexicographical “less than”), we multiply numbers by consecutive powers of two starting from the greatest one so the preceding terms are not “neutralized” by the next ones. Takie this example:

$\begin{gather*} A = \{ 0, 1, 1, 1, 1 \} \\ B = \{ 1, 0, 0, 1, 1 \} \\ y = -16 + 8 + 4 + 2 + 1 = -1 \end{gather*}$

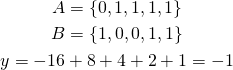
Even though only first one element is lower and all the others are greater in vector $A$ than in vector $B$ , the total value is still negative, thanks to powers of two.

How do we perform other comparisons? It is pretty simple:

$\begin{gather*} A \stackrel{?}{>=} B = y \stackrel{?}{>=} 0 \\ A \stackrel{?}{>} B = y \stackrel{?}{>} 0 \\ A \stackrel{?}{<=} B = y \stackrel{?}{<=} 0 \\ A \stackrel{?}{<} B = y \stackrel{?}{<} 0 \\ A \stackrel{?}{=} B = y \stackrel{?}{=} 0 \\ A \stackrel{?}{\neq } B = y \stackrel{?}{\neq} 0 \end{gather*}$

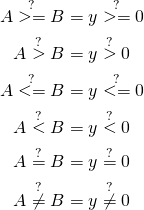
Longer vectors

We know how to compare vectors up to $30$ elements but how to compare longer ones? Well, the trick is: let’s do the same again.

Imagine that we have vectors with hundreds of elements. We take first $30$ elements and compare them lexicographically. We get one number which is negative, positive, or zero. The number represents relation of first $30$ elements of $A$ compared lexicographically with first $30$ elements of $B$ . We can now take next $30$ elements and compare them in the same way. Moving forward we finally get the following vector:

$\begin{gather*} C = \{ c_0, c_1, \ldots, c_p \}, c_0, \ldots, c_p \in \mathbb{Z} \\ p = \left\lfloor \log _{30} n \right \rfloor \end{gather*}$

This is another vector representing packages of $30$ elements of $A$ compared to $B$ . We can now compare $C$ with vector $D = \{ 0, 0, 0, \ldots, 0 \}$ of the same length.

Why does it work? Well, if first $30$ elements of $A$ are lexicographically lower than $30$ elements of $B$ , $c_0$ will be negative so next comparison will still work well since $c_0 < 0$ . If first $30$ elements are equal, $c_0 = 0$ so next batch of $30$ elements will have a chance to change the comparison result. If first elements are greater then $c_0 > 0$ which will determine the result.

We can recursively compare smaller and smaller vectors and finally end with just one number representing the solution. Finally, by comparing its sign we will be able to determine the final result.

Summary

As we can see, we are able to compare vectors much faster with hashing approach than by using naive one.