This is the seventeenth part of the ILP series. For your convenience you can find other parts in the table of contents in Part 1 – Boolean algebra

Hi all. Today we are going to solve another riddle, called Lonpos 505 Puzzle. It is very similar to the riddle from the previous part so you might want to read it first.

Table of Contents

Game

In the game we are given a set of 12 elements with different shapes:

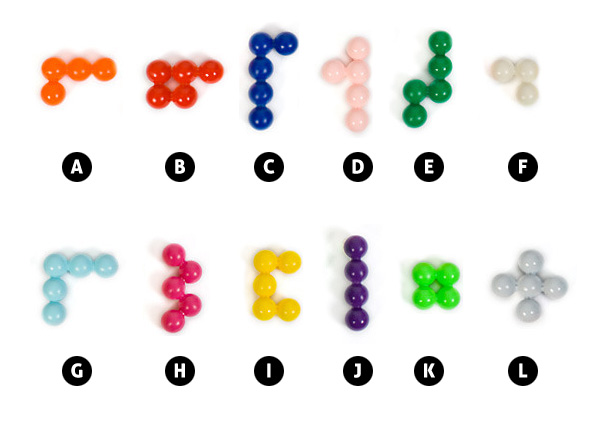
Elements

We are also give a starting position of elements:

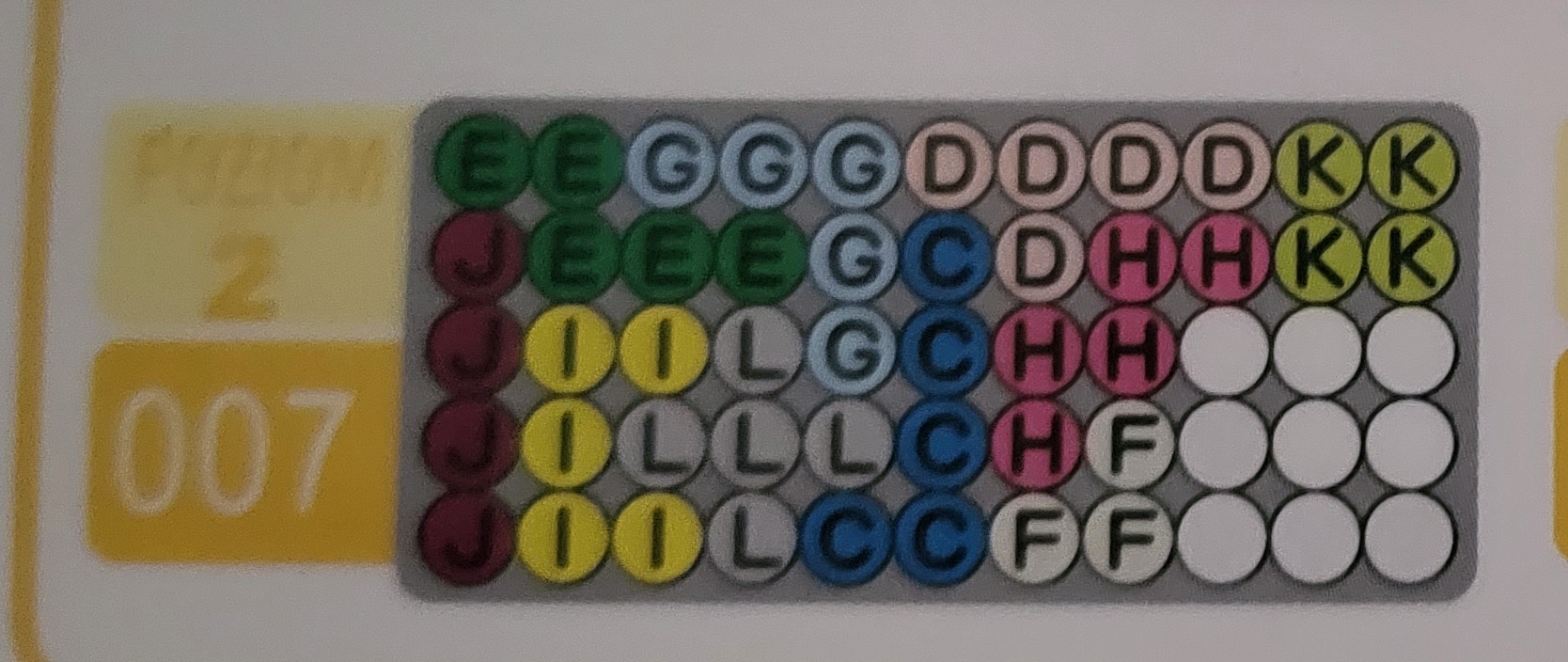
Starting position

Our goal is to add missing elements in a way that the board is filled completely:

Solution

Let’s begin.

Variables

Our board has 55 fields, we have 12 elements. For every field position $(x,y)$ and for every element $k$ we need variables representing placement of the element on the board, so we have the following binary variables:

$\begin{gather*} \displaystyle\mathop{\forall}_k \displaystyle\mathop{\forall}_{x,y} V_{k, x, y} \end{gather*}$

Just like in the previous part, variable being equal to one means that the following field is occupied by the element.

Shapes

Since every element has different shape, we will need a different set of constraints for different elements. For instance, element A has four pieces and can be placed in one out of eight positions (4 rotations on a plane and two rotations of the sides, see the pciture), whereas element K can be placed in exactly one way.
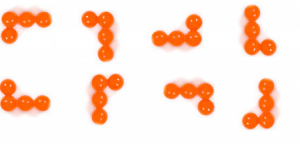
Rotations of element A
So we do the following:
For every position $(x,y)$ , for every element $k$ , and for every rotation of this element we need to choose variables representing placement of this element on the plane. For instance: let’s say that we want to place second rotation of element A in the position $(2,3)$ . We would need to consider the following variables:

$\begin{gather*} V_{1, 2, 3}\\ V_{1, 3, 3}\\ V_{1, 3, 4}\\ V_{1, 3, 5} \end{gather*}$

Next, we calculate conjunction of these variables. If it is true it means that all these fields are occupied by element one. This means:

$\begin{gather*} V_{1, 2, 2, 3} = V_{1, 2, 3} \wedge V_{1, 3, 3} \wedge V_{1, 3, 4} \wedge V_{1, 3, 5} \end{gather*}$

$V_{1,2,2,3}$ means element $1$ , rotation $2$ , position $(2,3)$ .
We calculate these variables for every rotation of every element placed on every possible position on the board.

Exactly one rotation of an element

Since we have multiple rotations for almost every element, we need to make sure that at most one rotation for given position is selected:

$\begin{gather*} \displaystyle\mathop{\forall}_k \displaystyle\mathop{\forall}_{x,y} R_{k,x, y} = \displaystyle\mathop{\sum}_{r} V_{k, r, x, y} \le 1 \end{gather*}$

What’s more, we need to select exactly one placement of an element, which means that we need to select exactly one rotation for particular element:

$\begin{gather*} \displaystyle\mathop{\forall}_k \displaystyle\mathop{\sum}_{x,y} R_{k,x, y} = 1 \end{gather*}$

Exactly one element in a position

If we would try to solve the problem right now, we would end up with exactly one rotation of all elements placed on the board, however, these elements would probably land all in the same place. We need to make sure that for every position there is exactly one piece of elements there:

$\begin{gather*} \displaystyle\mathop{\forall}_{x,y} \displaystyle\mathop{\sum}_{k,x,y} V_{k, x, y} = 1 \end{gather*}$

Starting position

If we want to solve the riddle for a given starting position, all we need to do is set subset of variables to one, as described in instruction.

Summary

As we can see, the implementation looks a bit simpler than in previous part. However, this problem is much more difficult than previous one because we have many more variables and much more difficult constraints. During my tests I was able to solve the problem easily when 8 elements were already placed on the board, however, I didn’t get any solution in an hour for a problem with only 4 elements placed on the board as a starting position. You can verify for yourself that this problem is not as easy as it looks like.

Bonus chatter: Lonpos 500 Puzzle is very interesting game. It also has version in 3D space — try to implement it using ILP.