This is the sixteenth part of the ILP series. For your convenience you can find other parts in the table of contents in Part 1 – Boolean algebra

Hi all. Today we are going to use ILP to solve a cube riddle. This will be a basic application of ILP approach because we are not going to define any meaningful cost function. All we want to get is any solution fulfilling provided constraints. Let’s go.

Table of Contents

Problem description

We have the following cube:
Cube 1
Cube 2
We have nine l-shape elements which we can use to build a bigger cube with a side of length three. Elements are identical, we can rotate them but we cannot change their shape.

This problem was posted as a question on 4programmers forum

For this problem we will utilize a so called zero-one linear programming. It is a special case of ILP with binary variables only. This approach is often used to solve decision problems for which we want to get any solution, disregarding the cost function.

Necessary variables

We start with defining necessary variables. We have nine elements, every element consists of three “pieces”. For each element we define a binary variables saying whether this element has piece in a specific cube position. So we end up with:

$\begin{gather*} P_{k, x, y, z} \end{gather*}$

where $k$ is a number of element (so it is from $1$ to $9$ ) and $x,y,z$ are coordinates of the cube. So we have $9 \cdot 3 \cdot 3 \cdot 3 = 243$ binary variables. Every variable is allowed to be zero or one. Zero means that the particular element has no piece in the specific coordinates.
Having these variables let’s start with adding constraints.

Three pieces for every element

We start with an obvious constraint. Every element should have exactly three pieces. This means the following:

$\begin{gather*} \displaystyle\mathop{\forall}_k \displaystyle\mathop{\sum}_{x, y, z} P_{k, x, y, z} = 3 \end{gather*}$

We sum for indexes which make sense. For every $k$ element we want the sum of variables for every coordinate for this element to be equal to three.

Stop tearing elements

If we would solve the problem right now, we would end up with elements scattered throughout the cube. Elements would probably be tore apart, however, all of them would have exactly three pieces.
In order to avoid tearing element apart, we need to make sure that its pieces are next to each other. We say that two pieces are one next to another when they are neighbours in one of three possible directions (along $x$ axis, along $y$ axis, along $z$ axis). We get the following constraint:

$\begin{gather*} \displaystyle\mathop{\forall}_k \displaystyle\mathop{\sum}_{x, y, z} P_{k, x, y, z} \cdot \left( P_{k, x+1, y, z} + P_{k, x, y+1, z} + P_{k, x, y, z+1} \right) = 2 \end{gather*}$

This formula means that for every piece $k$ and for every position $x, y, z$ we check whether position $x, y, z$ and any of its neighbouring positions are occupied by pieces of one element. If it is so, these variables will be equal to $1$ , so by multiplying them we will get $1$ . Since we deal with binary variables only, we can use just a conjunction defined in part 1.

Bending elements

If we would solve the problem right now, elements would have exactly three pieces, and pieces would be next to each other. However, we might end up with a straightened element, e.g., element with all pieces along one axis.
In order to avoid this, we need to add the following constraints:

$\begin{gather*} \displaystyle\mathop{\forall}_k \displaystyle\mathop{\forall}_{x, y} \displaystyle\mathop{\sum}_{z} P_{k, x, y, z} \le 2 \\ \displaystyle\mathop{\forall}_k \displaystyle\mathop{\forall}_{x, z} \displaystyle\mathop{\sum}_{y} P_{k, x, y, z} \le 2 \\ \displaystyle\mathop{\forall}_k \displaystyle\mathop{\forall}_{y, z} \displaystyle\mathop{\sum}_{x} P_{k, x, y, z} \le 2 \end{gather*}$

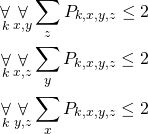
Let’s take the first one constraint. For every element $k$ and for every position $x,y$ on the bottom side of the cube we sum all elements along the $z$ axis. So we sum take all positions for one vertical line, sum their variables and make sure that there are at most two pieces on that line. Next two constraints do the same for $y$ axis and $x$ axis respectively.

Exactly one piece in one place

Once again, if we would solve the problem right now, we would end up with elements with correct shape (e.g., with three pieces and in l-shape), however, all this elements still might be in exactly the same place. In order to avoid that, we need to make sure that for every coordinate there is exactly one piece of exactly one element:

$\begin{gather*} \displaystyle\mathop{\forall}_{x, y, z} \displaystyle\mathop{\sum}_{k} P_{k, x, y, z} = 1 \end{gather*}$

For every position we sum variables for all elements and we require that this sum is equal to exactly one. This means that exactly one variable will be true.

Summary

As we can see, this riddle can be solved really straightforward. We start with required variables and add constraints to make our elements look more realistic. Finally, we put elements in places and build the actual cube.
I checked this naive implementation using CPLEX and the solver was able to find the solution in less than 200 miliseconds. Not bad.
Next time we are going to solve similar problem, however, we will need to deal with elements of different shapes. Stay tuned.