This is the eighteenth part of the ILP series. For your convenience you can find other parts in the table of contents in Part 1 – Boolean algebra
Hi! In this part of ILP series we start another series — Students Placement Problem. Today we will see the description of the problem and will try to introduce few definitions. In next parts we will formulate the problem using ILP and try to solve it.
Table of Contents
Students Placement Problem — Introduction
Imagine a university and students who want to enroll for oncoming courses. Usually the authorities of the university creates the timetable and give it to students, so they are assigned to fixed groups and (usually) cannot easily change their schedule. However, some universities approach the problem in different way — they only create basic schedule of lectures and classes. It is up to students how they create groups and choose classes which they prefer most. This approach is very flexible for students because they are able to easily attend classes and leisure time duties, however, it might be difficult for students to create groups in a way that everyone is happy. We call this problem of creating groups a “Students Placement Problem”.
University Timetable
At the beginning of each semester, the authorities of the university prepare a timetable of lectures, classes, and all other students’ activities. The timetable contains their starting and ending times (e.g., Algebra Class begins at 8:00 AM on Monday and ends at 10:00 AM the same day). Since there are many students and they are not able to attend the same class at once (e.g., because the room can be occupied by at most 20 students), the timetable consists of many instances of the same activity. For instance, Algebra Class might happen on Monday, Tuesday, and Thursday, so at most 60 students are able to attend the classes. Students can choose class which suits them most.
By a “course” we understand a course at university, e.g., Algebra, Calculus etc. By a “class” we understand single instance of class within the course. For instance, Algebra course might have three classes: on Monday, Tuesday, and on Thursday. Every “class” has assigned begin time, end time, upper limit for number of attending students, lecturer, room, and all other things which are required by the class.
Having such a timetable, our goal is to calculate the placement of students in a way that they are “happy”. We will define happiness in one of the next parts. We need to consider some formal requirements — e.g., maximum number of students which can fit the room — but the final assignment is up to us. The authorities of the university do not impose any restrictions on the form of final students’ schedules. For instance, students are not bound to attend the university every day or start classes at 8:00 AM.
To sum up. We are given a general timetable of classes and calculate the allocation of students to make everyone happy. This is our goal. And, one more thing, we are going to use ILP.
Some definitions
We introduce the following definitions:
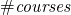 — total number of courses
— total number of courses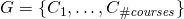 — general schedule consisting courses
— general schedule consisting courses- Every course
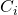 has
has 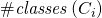 classes
classes - Every course
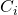 is defined as a set of classes:
is defined as a set of classes: 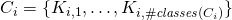
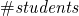 — number of students
— number of students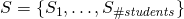 — set of students
— set of students- Every student
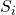 is defined as a
is defined as a 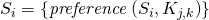 — a set of preferences for student
— a set of preferences for student 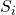 for classes in courses
for classes in courses
For the sake of brevity we assume that every student is registered for every course. It is just an implementation detail.
Preferences
We need to define one more thing. Since we want to maximize happiness of students, we need to have some metric to be able to represent their happiness using numbers. We do it in the following way: for every class we ask every student to give a number from zero to ten representing his or her preference to be assigned to this class. Value of ten means that the student would love to be assigned to this particular class, value zero means the opposite — student really doesn’t want to be assigned to this instance. We also give students possibility to mark some classes as impossible for them. This means that the student ins physically unable to attend the class (e.g., because of other duties).
Having this preferences, our goal is to make students as happy as possible. As we will see soon, we can calculate the happiness in many different ways. For now you can intuitively assume that we want to give students classes with higher preferences points.
Summary
In the next part we are going to define part of necessary constraints and variables to represent the problem using ILP. See you soon.