This is the fifteenth part of the ILP series. For your convenience you can find other parts in the table of contents in Part 1 – Boolean algebra
Today we are going to use comparisons to implement few basic set operations. Let’s go.
Table of Contents
In set, Not in set
We start with In set operation. For set ![]() and value
and value ![]() we want to ask whether
we want to ask whether ![]() is in set
is in set ![]() . This is very easy because all we need to do is compare
. This is very easy because all we need to do is compare ![]() with all values from set and calculate the sum:
with all values from set and calculate the sum:
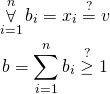
For every value we calculate variable ![]() which is true when
which is true when ![]() is equal to
is equal to ![]() . Next, we sum all values and check whether the sum is positive. If it is true then
. Next, we sum all values and check whether the sum is positive. If it is true then ![]() is true which means that
is true which means that ![]() is in set
is in set ![]() .
.
For operation Not in set we do almost the same. The only difference is in comparing the sum with ![]() .
.
Different values count
Very similar operation is a Different values count. For multiset (e.g., set with repetitions) ![]() we want to ask how many different values does it contain. The formula is as follows:
we want to ask how many different values does it contain. The formula is as follows:
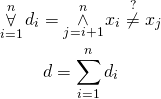
For every variable ![]() we check whether all variables with indexes greater than
we check whether all variables with indexes greater than ![]() are different than
are different than ![]() . Basically, we traverse multiset
. Basically, we traverse multiset ![]() in some arbitrary order and for
in some arbitrary order and for ![]() -th value we check whether all remaining values are different.
-th value we check whether all remaining values are different.
All different
We can use previous formula to make sure that all values in mulitset are different (so the multiset is in fact set). To achieve that we need to calculate different values count ![]() and add constraint
and add constraint ![]() where
where ![]() is a number of variables in a multiset.
is a number of variables in a multiset.
Summary
Today we implemented useful set operations. Next time we are going to utilize all ILP knowledge to solve real problem — we will be solving a simple cube riddle.