This is the seventh part of the ILP series. For your convenience you can find other parts in the table of contents in Part 1 – Boolean algebra

We have already seen how to multiply variables in ILP. In part 5 we saw how to define minimum and absolute value. Last time we improved our multiplication algorithm. Today we are going to handle negative numbers.

Table of Contents

General idea

First let’s summarize what we can do already:

We are able to decompose variable and extract its digits
We can multiply two binary digits by calculating their conjunction
We know how to multiply non-negative number by single binary digit using minimum function
We can multiply two non-negative numbers by decomposing latter argument, multiplying its digits by former argument and power of two, and summing the results
We know how to compare numbers and so we are able to deduce whether a number is negative (by comparing it with zero)

We would like to multiply possibly negative numbers. We will do that by multiplying their absolute values (so ignoring the sign) and then changing the sign if necessary.

First step – multiplying absolute values

We start with the following variables:

$\begin{gather*} a, b, x \in \mathbb{Z} \\ k = 2^n - 1 \\ n \in \mathbb{N} \\ \left|a\right|, \left|b\right|, \left|x\right| \le k \\ b_0, b_1, \ldots, b_{n-1} \in \{0, 1\} \end{gather*}$

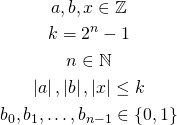
We have arguments ( $a,b$ ), result ( $x$ ), upper bound ( $k$ ), and digits of $b$ . We first define:

$\begin{gather*} a_+ = \left|a\right| \\ b_+ = \left|b\right| \\ x_+ = a \cdot b \end{gather*}$

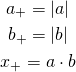
Here we multiply variables by using already described algorithms.

Second step – calculating the sign

Next, we calculate the sign:

$\begin{gather*} a_s = a \stackrel{?}{\ge} 0 \\ b_s = b \stackrel{?}{\ge} 0 \\ s = a_s \stackrel{?}{=} b_s \end{gather*}$

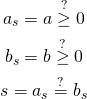
$s$ will be one only when $a_s$ and $b_s$ have the same sign (so they are both negative or both positive). When the arguments have different signs, $s$ will be equal to zero.

Final step – changing the sign of the result

Now we are going to set the sign of the result. We multiply the result of multiplication of absolute values by the sign:

$x_s = \min(x_+, s \cdot k)$

When the sign $s$ is equal to one the $x_s$ will be equal to $x_+$ . Otherwise, it will be equal to zero.
Now we are going to set the final result using this formula:

$x = \left(x_s - \frac{x_+}{2}\right) \cdot 2$

When the result should be non-negative, the sign $s$ will be equal to one, so the $x_s$ will be equal to $x_+$ , and we will get $\left(x_+ - \frac{x_+}{2}\right) \cdot 2 = \frac{x_+}{2}\cdot 2 = x_+$ . However, when the result should be negative, the sign will be zero, the $x_s$ will be equal to zero, and we will get $\left(0 - \frac{x_+}{2}\right) \cdot 2 = -\frac{x_+}{2} \cdot 2 = -x_+$ .

Division poses multiple difficulties. First, it may introduce representation errors since we need to use fractions. Second, some solvers do not support non-integer values at all so they cannot multiply negative variables. There are ways to avoid division completely and we should use them if possible.

Changing the result sign with maximum and minimum

Instead of dividing we can use maximum and minimum. This formula is a basic extension of multiplication by a binary digit:

$x = \min\left(x_+, s \cdot k\right) + \max\left(-x_+, -\left(1-s\right) \cdot k\right)$

When the result should be positive then $s$ is equal to one and first component of the sum is equal to $x_+$ . Second part of the sum is equal to zero as we take maximum of some negative number and zero. Hence the whole sum is equal to $x_+$ which is as expected.

However, when $s$ is equal to zero and the result should be negative, first part of the sum is equal to zero because we take minimum of $x_+$ and zero. Second part of the sum is equal to $-x_+$ because we take maximum of $-x_+$ and very small number.

Changing the result sign with subtraction

We can calculate the final result even easier using subtraction:

$x = x_+ \cdot s - x_+ \cdot \left(1 - s\right)$

If the result should be non-negative then $s$ is equal to one so the formula simplifies to $x_+ \cdot 1 - x_+ \cdot 0 = x_+$ . However, when result should be non-postive and $s$ is equal to zero then we obtain $x_+ \cdot 0 - x_+ \cdot 1 = -x_+$ .

This is simple and elegant, and it doesn’t introduce unnecessary floating point issues.

Summary

We are now able to multiply any integer variables for which we know upper and lower bound. In the next part we will use this operation to calculate greatest common divisor (GCD).