This is the eighth part of the ILP series. For your convenience you can find other parts in the table of contents in Part 1 – Boolean algebra

Today we are going to implement multiple and Greatest Common Divisor (GCD) using ILP. Representations of these functions look very trivial, however, they are in fact a bit difficult in practice. Let’s begin.

Table of Contents

First step – multiple

We will start with the following requirement: having variable $a$ , we want the variable $b$ to be a multiple of $a$ . This means that for the variables $a, b \in \mathbb{Z}$ we want $a$ to be a divisor of $b$ . For instance, for $a = 15$ we want $b$ to be equal $0$ , or $15$ , or $30$ , or $-15$ , or $-30$ , or something else (I hope you get the rule). It is in fact easy using helper variable. The formula is:

$\begin{gather*} a, b \in {Z} \\ t \in {Z} \\ b = a \cdot t \end{gather*}$

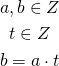
We already know how to multiply negative values so we are able to calculate this. Of course we need to set upper bound for variables.

Greatest Common Divisor

Now we are going to implement GCD. As you remember from school, greatest common divisor is a divisor with maximum possible value. We will now use only non-negative variables since GCD is usually defined only for them.

First part – any common divisor

Let’s start with first approach: for variables $a, b$ we would like to define $g = \gcd(a, b)$ :

$\begin{gather*} a, b, g \in {N_{+}} \\ t_1, t_2 \in {N_{+}} \\ a = g \cdot t_1 \\ b = g \cdot t_2 \end{gather*}$

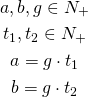
This works only partially. For instance, for $a = 24, b = 20$ we might get $g = 4$ (which is fine), but we might also get $g = 2$ . The latter value fulfills the constraints but it is not the value we are looking for because we want to find the greatest possible value.

Second part – greatest common divisor

To make sure that we get GCD we will use Bézout’s identity. It says that we can represent every multiple of $g = \gcd(a,b)$ as $ax + by = g$ . We can add this formula to the previously defined and get the following:

$\begin{gather*} a, b, g \in {N_{+}} \\ t_1, t_2 \in {N_{+}} \\ x, y \in {Z} \\ a = g \cdot t_1 \\ b = g \cdot t_2 \\ g = a \cdot x + b \cdot y \end{gather*}$

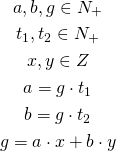
This works as follows: first we define that $a$ and $b$ are both multiple of $g$ . This means that $g$ is any common divisor and is not greater than GCD of $a$ and $b$ . The last part says that $g$ is a multiple of GCD of $a$ and $b$ . Since $g$ is a positive variable, the only value fulfilling all the requirements is $g = \gcd(a,b)$ !

Problems with the implementation

The formula for GCD looks very trivial, however, there are problems with this approach. First, $x$ and $y$ might be very big (much bigger than $a$ and $b$ ). Because we need to know the upper bound of values, we need to be very careful what we are going to calculate. What’s more, this is very difficult to solve and many solvers are not capable of doing that. I have checked Gurobi, CPLEX, LpSolve, Microsoft Solver Foundation, and SCIP, and in fact I was able to calculate GCD of very small numbers only (less than $20$ ). For bigger values the solvers were returning incorrect results or even saying that there is no solution. So in theory it works, however, in practice it is rather unreliable.