This is the fifty third part of the ILP series. For your convenience you can find other parts in the table of contents in Part 1 – Boolean algebra
Today we are going to implement Maximum flow in ILP.
We use the following graph:
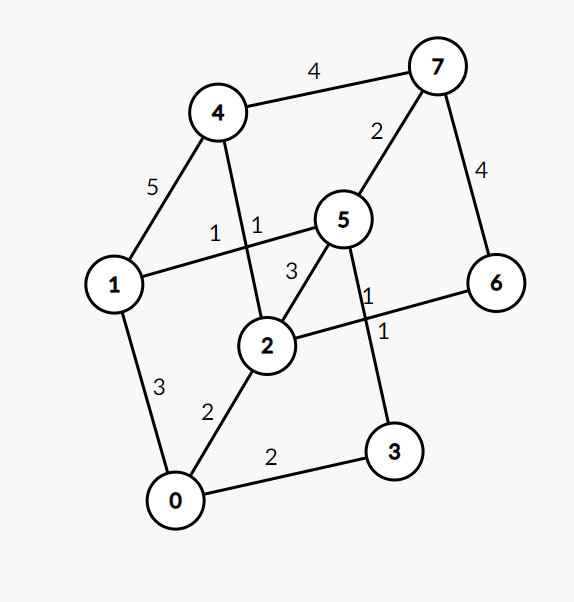
We use the following records:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
class Vertex { public List<Edge> Edges { get; set; } public string Name { get; set; } public Vertex() { Edges = new List<Edge>(); } } class Edge { public IVariable Flow { get; set; } public Vertex A { get; set; } public Vertex B { get; set; } public int Capacity { get; set; } } |
Let’s now initialize the graph:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 |
Vertex v0 = new Vertex { Name = "0" }; Vertex v1 = new Vertex { Name = "1" }; Vertex v2 = new Vertex { Name = "2" }; Vertex v3 = new Vertex { Name = "3" }; Vertex v4 = new Vertex { Name = "4" }; Vertex v5 = new Vertex { Name = "5" }; Vertex v6 = new Vertex { Name = "6" }; Vertex v7 = new Vertex { Name = "7" }; Edge e01 = new Edge { Capacity = 3, A = v0, B = v1 }; Edge e02 = new Edge { Capacity = 2, A = v0, B = v2 }; Edge e03 = new Edge { Capacity = 2, A = v0, B = v3 }; Edge e14 = new Edge { Capacity = 5, A = v1, B = v4 }; Edge e15 = new Edge { Capacity = 1, A = v1, B = v5 }; Edge e24 = new Edge { Capacity = 1, A = v2, B = v4 }; Edge e25 = new Edge { Capacity = 3, A = v2, B = v5 }; Edge e26 = new Edge { Capacity = 1, A = v2, B = v6 }; Edge e35 = new Edge { Capacity = 1, A = v3, B = v5 }; Edge e47 = new Edge { Capacity = 4, A = v4, B = v7 }; Edge e57 = new Edge { Capacity = 2, A = v5, B = v7 }; Edge e67 = new Edge { Capacity = 4, A = v6, B = v7 }; v0.Edges.Add(e01); v0.Edges.Add(e02); v0.Edges.Add(e03); v1.Edges.Add(e14); v1.Edges.Add(e15); v2.Edges.Add(e24); v2.Edges.Add(e25); v2.Edges.Add(e26); v3.Edges.Add(e35); v4.Edges.Add(e47); v5.Edges.Add(e57); v6.Edges.Add(e67); var solver = new CplexMilpSolver(10); var edges = new[] { e01, e02, e03, e14, e15, e24, e25, e26, e35, e47, e57, e67 }; foreach (var edge in edges) { edge.Flow = solver.CreateAnonymous(Domain.PositiveOrZeroInteger); } var vertices = new[] { v0, v1, v2, v3, v4, v5, v6, v7 }; |
Now we need to add two constraints.
First one limits the flow for a given edge — we cannot exceed the capacity link:
|
1 2 3 4 5 |
// Flow of a link cannot exceed capacity of that link foreach (var edge in edges) { edge.Flow.Set(ConstraintType.LessOrEqual, solver.FromConstant(edge.Capacity)); } |
Second constraint says that whatever flows into the node must flow out of it. Input flow must be equal to output flow:
|
1 2 3 4 5 6 |
// Incoming node flow is equal to outgoing flow node foreach (var vertex in vertices.Except(new []{v0, v7})) { solver.Operation(OperationType.Addition, edges.Where(e => e.B == vertex).Select(e => e.Flow).ToArray()) .Set(ConstraintType.Equal, solver.Operation(OperationType.Addition, edges.Where(e => e.A == vertex).Select(e => e.Flow).ToArray())); } |
Now we need to solve the program:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
IVariable cost = solver.Operation(OperationType.Addition, e01.Flow, e02.Flow, e03.Flow).MakeGoal(GoalType.Maximize); solver.AddGoal("Cost", cost); solver.Solve(); Console.WriteLine("Edges"); foreach (var edge in edges) { Console.WriteLine(solver.GetValue(edge.Flow)); } Console.WriteLine("Cost"); Console.WriteLine(solver.GetValue(cost)); |
That’s it.