This is the thirty sixth part of the ILP series. For your convenience you can find other parts in the table of contents in Part 1 – Boolean algebra
Today we will try to introduce various goal types to our problems. There are six main types of optimizations: maximizing, minimizing, maximizing maximum, maximizing minimum, minimizing maximum, and minimizing minimum. Let’s go.
Table of Contents
Maximizing and minimizing
These two are pretty easy. First of all, our solver needs to be able to optimize our cost function, usually minimize it. Imagine that we have minimizing of function ![]() out of the box. In order to maximize this function, we simply need to negate it:
out of the box. In order to maximize this function, we simply need to negate it: ![]() . It also works the other way round: if we have maximizing in our solver, we can negate function to have minimization problem.
. It also works the other way round: if we have maximizing in our solver, we can negate function to have minimization problem.
Maximize minimum and minimize maximum
These two looks difficult but are in fact very easy. Let’s assume, that we are able to maximize cost function. We have variables ![]() and we want to maximize minimum of them. We could do something like
and we want to maximize minimum of them. We could do something like ![]() since we already know how to calculate maximum of variables, but there is a better way. We introduce another variable
since we already know how to calculate maximum of variables, but there is a better way. We introduce another variable ![]() and add the following constraints:
and add the following constraints:
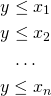
And now we maximize function ![]() . How does it work? Well, since
. How does it work? Well, since ![]() must be less or equal than all
must be less or equal than all ![]() , solver needs to take care of fulfilling these constraints. At the same time, solver has to maximize goal function which will indirectly maximize minimum of variables.
, solver needs to take care of fulfilling these constraints. At the same time, solver has to maximize goal function which will indirectly maximize minimum of variables.
Minimizing maximum works the same way: we introduce another variable, add constraints (this time “greater or equal”) and minimize the variable.
Maximize maximum and minimize minimum
These two goals are difficult because there is no shortcut. Let’s take first one: maximizing maximum. We have variable ![]() . We introduce another variable
. We introduce another variable ![]() and try to match it with one of the other variables:
and try to match it with one of the other variables:
![]()
And now we maximize ![]() . Minimizing minimum works the same way.
. Minimizing minimum works the same way.
Summary
If we constrain variable just to use it in cost function, it is usually possible to use some clever tricks to calculate result. For instance, when maximizing minimum we could just calculate minimum of variables (using ![]() operation) and maximize the result, but it would be much more computationally expensive. Always look for trick which will reduce size of your problem.
operation) and maximize the result, but it would be much more computationally expensive. Always look for trick which will reduce size of your problem.