This is the twenty ninth part of the ILP series. For your convenience you can find other parts in the table of contents in Part 1 – Boolean algebra
Hello! Today we are going to solve nonograms using ILP.
Table of Contents
Task description
Nonograms are picture logic puzzles in which cells in a grid must be colored or left blank according to numbers at the side of the grid to reveal a hidden picture. Images are usually black and white, however, they can be colored. Below is an example of a nonogram (by wikipedia):
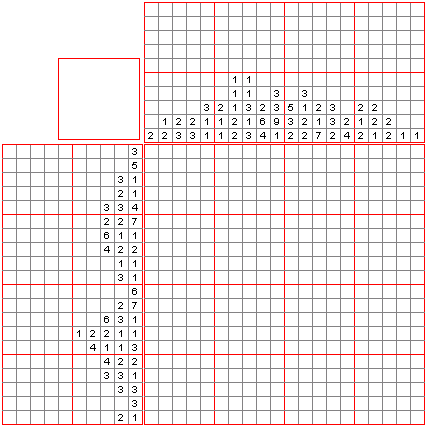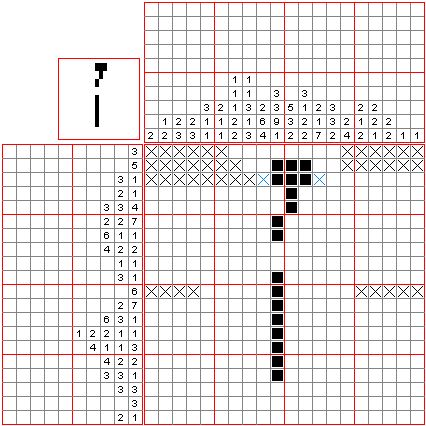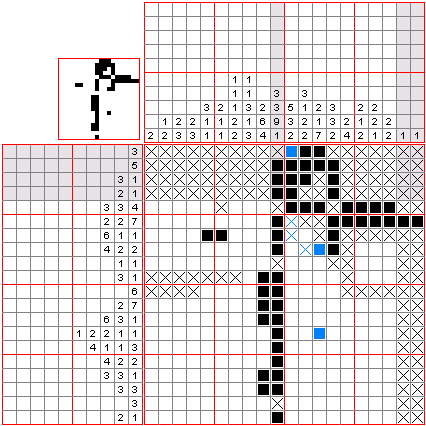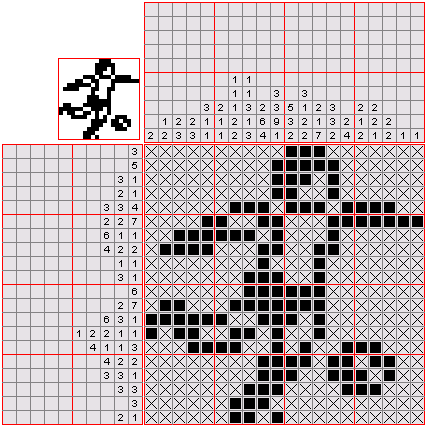
We will solve black and white nonogram, so we assume that numbers describe blocks of black fields whit at least one white field between every block.
Variables
As with most of the riddles we start with defining binary variables representing decisions. Let’s assume that the picture has size ![]() (width and height). For every field we define a binary variable meaning whether we fill this field or no:
(width and height). For every field we define a binary variable meaning whether we fill this field or no:
![]()
We also need to define variables representing top-left blocks’ corners. Let’s introduce the following notation: ![]() means number of blocks in
means number of blocks in ![]() -th column,
-th column, ![]() means length of
means length of ![]() -th block in
-th block in ![]() -th column. Analogously,
-th column. Analogously, ![]() means number of block in
means number of block in ![]() -th row,
-th row, ![]() means length of
means length of ![]() -th block in
-th block in ![]() -th row. We define the following binary variables:
-th row. We define the following binary variables:
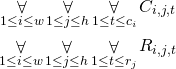
Variable ![]() means whether
means whether ![]() -th block in
-th block in ![]() -th column starts (e.g., its top-left field is) in field
-th column starts (e.g., its top-left field is) in field ![]() . Analogously,
. Analogously, ![]() means whether
means whether ![]() -th block in
-th block in ![]() -th row starts in field
-th row starts in field ![]() .
.
After solving the problem we obtain the solution from variables ![]() . Other variables are used only to specify constraints.
. Other variables are used only to specify constraints.
Constraints
We start with two obvious constraints: number of selected fields in each row and each column must match the blocks’ lengths:
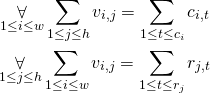
Now we need to make sure that in every field there starts at most one block:
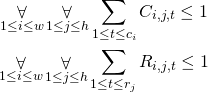
Next, we need to make sure that if the block starts in particular field, all fields of this block are selected:
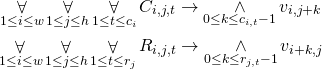
When a particular column block starts in field ![]() (which means that
(which means that ![]() is true) then all fields
is true) then all fields ![]() must be true so we use conjunction. The same idea goes for row blocks. We also need to make sure that block does not start close to the boundary:
must be true so we use conjunction. The same idea goes for row blocks. We also need to make sure that block does not start close to the boundary:
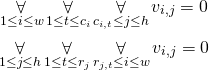
Finally, we need to take care of blocks ordering. We need to make sure that block occur in proper order. We use the following idea: if some column block starts in field ![]() which means that
which means that ![]() is true, previous block must start in some field
is true, previous block must start in some field ![]() where
where ![]() . So the sum of variables indicating start of the block must be true. The following constraints take care of this:
. So the sum of variables indicating start of the block must be true. The following constraints take care of this:
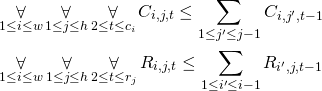
If ![]() is true then sum of
is true then sum of ![]() must be true in order to fulfill the constraint. On the other hand, if
must be true in order to fulfill the constraint. On the other hand, if ![]() is false, then sum of
is false, then sum of ![]() can have any value. The same goes for rows.
can have any value. The same goes for rows.
Summary
As we can see implementation is rather easy. The most difficult part is related to ordering the blocks, the rest is pretty straightforward. Next time we will solve sudoku.