This is the one hundred and fourth part of the ILP series. For your convenience you can find other parts in the table of contents in Part 1 – Boolean algebra
Today we are going to solve the 12 Stones Logic Puzzle. We have 12 stones, 11 of them are of equal weight, 1 is of unequal weight (could be lighter or heavier). We can use at most 3 weightings on a balance scale to find the odd stone and tell whether it’s lighter or heavier.
That’s gonna be a little bit tricky to understand, but let’s try it out. We want to implement an ILP model that will give us a recipe for finding the odd stone. Notice, that this problem seems to be even harder than NP class because we can’t verify the solution in polynomial time.
The idea is as follows:
- We create 24 lists. Each list contains exactly 3 integers. Each integer indicates which subset of stones to put on the left side of the scale, and which stones to put on the right side of the scale.
- Each list is supposed to determine the “designated stone”, so provide the weightings that will determine that the stone number
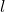 is lighter (heavier).
is lighter (heavier). - For each list, we calculate the results of weightings for every possible input (which stone is odd and how). This gives us a three dimensional list of
[listId][number of weighting][which stone is odd and how]. - For each list, we make sure that we get unique weighting results for the “designated stone” of that list (so results of weightings for that list for other stones must be different).
- Each list must expect unique result of weightings.
- When two lists have the same prefix of how to put stones and what result to expect for
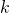 first steps, then their
first steps, then their 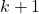 -th step must be the same (to have deterministic solution).
-th step must be the same (to have deterministic solution).
That was quite a lot. Let’s see the code:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 |
var stonesCount = 12; var weightingsCount = 3; var needToFindIfHeaverOrLigher = true; // -------------------------------------------------------- // [listId][whichWeighting][whichStone][wasLeftLighter + wasRightLighter + wasEqual] var weightingResultsCount = 3; var weightingResults = Enumerable.Range(0, 2*stonesCount).Select(listId => // Number of weighting Enumerable.Range(0, weightingsCount).Select(weighting => // stone 1 lighter, stone 1 heavier, stone 2 lighter, stone 2 heavier, ... Enumerable.Range(0, 2 * stonesCount).Select(stoneId => // wasLeftLighter, wasRightLighter, wasEqual Enumerable.Range(0, weightingResultsCount).Select(resultId => solver.CreateAnonymous(Domain.BinaryInteger) ).ToArray() ).ToArray() ).ToArray() ).ToArray(); // For each list, for each weighting, for each stone, exactly one result is possible for(int listId = 0; listId < 2 * stonesCount; ++listId){ for(int weighting = 0; weighting < weightingsCount; ++weighting){ for(int stoneId = 0; stoneId < 2 * stonesCount; ++stoneId){ solver.Operation<Addition>(weightingResults[listId][weighting][stoneId]).Set<Equal>(solver.FromConstant(1)); } } } // [listId][whichWeighting][putOnLeft, putOnRight] // Stone 1 lighter, stone 1 heavier, stone 2 lighter, stone 2 heavier, stone 3 lighter... var weightingLists = Enumerable.Range(0, 2*stonesCount).Select(listId => // Number of weighting Enumerable.Range(0, weightingsCount).Select(weighting => // stone 1 on left, stone 2 on left, stone 3 on left, ..., stone #stonesCount on left, stone 1 on right... Enumerable.Range(0, 2 * stonesCount).Select(stoneId => solver.CreateAnonymous(Domain.BinaryInteger) ).ToArray() ).ToArray() ).ToArray(); // For each list, for each weighting, make sure that we put some stone on the scale for(int listId = 0; listId < 2 * stonesCount; ++listId){ for(int weighting = 0; weighting < weightingsCount; ++weighting){ solver.Operation<Addition>(weightingLists[listId][weighting]).Set<GreaterOrEqual>(solver.FromConstant(1)); } } // For each list, for each weighting, make sure that each stone is either on the left, or on the right, or nowhere for(int listId = 0; listId < 2 * stonesCount; ++listId){ for(int weighting = 0; weighting < weightingsCount; ++weighting){ for(int stoneId = 0; stoneId < stonesCount; ++stoneId){ solver .Operation<Addition>(weightingLists[listId][weighting][stoneId], weightingLists[listId][weighting][stonesCount + stoneId]) .Set<LessOrEqual>(solver.FromConstant(1)); } } } // For each list, for each weighting, calculate the result based on the known input for(int listId = 0; listId < 2 * stonesCount; ++listId){ for(int weighting = 0; weighting < weightingsCount; ++weighting){ for(int stoneId = 0; stoneId < 2 * stonesCount; ++stoneId){ var stonesCountOnTheLeft = solver.Operation<Addition>(weightingLists[listId][weighting].Take(stonesCount).ToArray()); var stonesCountOnTheRight = solver.Operation<Addition>(weightingLists[listId][weighting].Skip(stonesCount).Take(stonesCount).ToArray()); var isThisListForLighterCase = stoneId % 2 == 0; var hasSpecialStoneOnLeft = weightingLists[listId][weighting][stoneId/2]; var hasSpecialStoneOnRight = weightingLists[listId][weighting][stonesCount + stoneId/2]; // Left has fewer stones (left is lighter) solver.Operation<MaterialImplication>( stonesCountOnTheLeft.Operation<IsLessThan>(stonesCountOnTheRight), weightingResults[listId][weighting][stoneId][0] ).Set<Equal>(solver.FromConstant(1)); // Right has fewer stones (right is lighter) solver.Operation<MaterialImplication>( stonesCountOnTheLeft.Operation<IsGreaterThan>(stonesCountOnTheRight), weightingResults[listId][weighting][stoneId][1] ).Set<Equal>(solver.FromConstant(1)); // Have equal stones if(isThisListForLighterCase){ // Lighter stone is on the left (left is lighter) solver.Operation<MaterialImplication>( stonesCountOnTheLeft.Operation<IsEqual>(stonesCountOnTheRight) .Operation<Conjunction>(hasSpecialStoneOnLeft), weightingResults[listId][weighting][stoneId][0] ).Set<Equal>(solver.FromConstant(1)); // Lighter stone is on the right (right is lighter) solver.Operation<MaterialImplication>( stonesCountOnTheLeft.Operation<IsEqual>(stonesCountOnTheRight) .Operation<Conjunction>(hasSpecialStoneOnRight), weightingResults[listId][weighting][stoneId][1] ).Set<Equal>(solver.FromConstant(1)); // There is no lighter stone here (are equal) solver.Operation<MaterialImplication>( stonesCountOnTheLeft.Operation<IsEqual>(stonesCountOnTheRight) .Operation<Conjunction>(hasSpecialStoneOnLeft.Operation<BinaryNegation>(), hasSpecialStoneOnRight.Operation<BinaryNegation>()), weightingResults[listId][weighting][stoneId][2] ).Set<Equal>(solver.FromConstant(1)); }else { // Heavier stone is on the left (righti s lighter) solver.Operation<MaterialImplication>( stonesCountOnTheLeft.Operation<IsEqual>(stonesCountOnTheRight) .Operation<Conjunction>(hasSpecialStoneOnLeft), weightingResults[listId][weighting][stoneId][1] ).Set<Equal>(solver.FromConstant(1)); // Heavier stone is on the right (left is lighter) solver.Operation<MaterialImplication>( stonesCountOnTheLeft.Operation<IsEqual>(stonesCountOnTheRight) .Operation<Conjunction>(hasSpecialStoneOnRight), weightingResults[listId][weighting][stoneId][0] ).Set<Equal>(solver.FromConstant(1)); // There is no heavier stone here (are equal) solver.Operation<MaterialImplication>( stonesCountOnTheLeft.Operation<IsEqual>(stonesCountOnTheRight) .Operation<Conjunction>(hasSpecialStoneOnLeft.Operation<BinaryNegation>(), hasSpecialStoneOnRight.Operation<BinaryNegation>()), weightingResults[listId][weighting][stoneId][2] ).Set<Equal>(solver.FromConstant(1)); } } } } // For each list pair, for each prefix length, check if prefixes are the same and the weighting results are the same, then next step must be the same for(int listId = 0; listId < 2 * stonesCount; ++listId){ for(int listId2 = listId + 1; listId2 < 2 * stonesCount; ++listId2){ var arePrefixesEqual = solver.FromConstant(1); for(int prefixLength = 0; prefixLength < weightingsCount; ++ prefixLength){ for(int stoneId = 0; stoneId < 2*stonesCount; ++stoneId){ solver .Operation<MaterialImplication>( arePrefixesEqual, weightingLists[listId][prefixLength][stoneId].Operation<IsEqual>(weightingLists[listId2][prefixLength][stoneId]) ).Set<Equal>(solver.FromConstant(1)); } for(int stoneId = 0; stoneId < 2*stonesCount; ++stoneId){ arePrefixesEqual = arePrefixesEqual.Operation<Conjunction>( weightingLists[listId][prefixLength][stoneId].Operation<IsEqual>(weightingLists[listId2][prefixLength][stoneId]) ); } for(int weightingResult = 0; weightingResult < weightingResultsCount; ++weightingResult){ arePrefixesEqual = arePrefixesEqual.Operation<Conjunction>( weightingResults[listId][prefixLength][listId][weightingResult] .Operation<IsEqual>(weightingResults[listId2][prefixLength][listId2][weightingResult]) ); } } } } // All list pairwise must have different expected stones and results for(int listId = 0; listId < 2 * stonesCount; ++listId){ for(int listId2 = listId + 1; listId2 < 2 * stonesCount; ++listId2){ if(needToFindIfHeaverOrLigher == false && listId % 2 == 0 && listId2 == listId + 1){ continue; } var areBothEqual = solver.FromConstant(1); for(int weighting = 0; weighting < weightingsCount; ++ weighting){ for(int stoneId = 0; stoneId < 2*stonesCount; ++stoneId){ areBothEqual = areBothEqual.Operation<Conjunction>( weightingLists[listId][weighting][stoneId].Operation<IsEqual>(weightingLists[listId2][weighting][stoneId]) ); } for(int weightingResult = 0; weightingResult < weightingResultsCount; ++weightingResult){ areBothEqual = areBothEqual.Operation<Conjunction>( weightingResults[listId][weighting][listId][weightingResult].Operation<IsEqual>(weightingResults[listId2][weighting][listId2][weightingResult]) ); } } areBothEqual.Set<Equal>(solver.FromConstant(0)); } } // For each list, the designated stone must have different results than results for other stones for(int listId = 0; listId < 2 * stonesCount; ++listId){ for(int otherList = 0; otherList < 2 * stonesCount; ++otherList){ if(listId == otherList){ continue; } if(needToFindIfHeaverOrLigher == false && ((listId % 2 == 0 && otherList == listId + 1) || (listId % 2 == 1 && otherList == listId - 1))){ continue; } var areBothEqual = solver.FromConstant(1); for(int weighting = 0; weighting < weightingsCount; ++ weighting){ for(int weightingResult = 0; weightingResult < weightingResultsCount; ++weightingResult){ areBothEqual = areBothEqual.Operation<Conjunction>( weightingResults[listId][weighting][listId][weightingResult].Operation<IsEqual>(weightingResults[listId][weighting][otherList][weightingResult]) ); } } areBothEqual.Set<Equal>(solver.FromConstant(0)); } } solver.AddGoal("goal", solver.FromConstant(0)); solver.Solve(); for(int listId = 0; listId < 2 * stonesCount; ++listId){ Console.Write("Stone {0} {1}: ", listId/2 + 1, listId %2 == 0 ? "lighter" : "heavier"); for(int weighting = 0; weighting < weightingsCount; ++weighting){ var stonesOnTheLeft = string.Join(",", Enumerable .Range(0, stonesCount) .Select(stoneId => Tuple.Create(stoneId + 1, Math.Round(solver.GetValue(weightingLists[listId][weighting][stoneId])) > 0.5)) .Where(tuple => tuple.Item2) .Select(tuple => tuple.Item1)); var stonesOnTheRight = string.Join(",", Enumerable .Range(0, stonesCount) .Select(stoneId => Tuple.Create(stoneId + 1, Math.Round(solver.GetValue(weightingLists[listId][weighting][stonesCount + stoneId])) > 0.5)) .Where(tuple => tuple.Item2) .Select(tuple => tuple.Item1)); var weightingResult = Math.Round(solver.GetValue(weightingResults[listId][weighting][listId][0])) > 0.5 ? ">" : Math.Round(solver.GetValue(weightingResults[listId][weighting][listId][1])) > 0.5 ? "<" : Math.Round(solver.GetValue(weightingResults[listId][weighting][listId][2])) > 0.5 ? "=" : "Something very wrong!"; Console.Write("({0} ; {1}) [{2}] ; ", stonesOnTheLeft, stonesOnTheRight, weightingResult); } Console.WriteLine(); } |
We set initial conditions in lines 1-3.
Next, we create the variables for weighting results (lines 7-20). That’s the four dimensional array. First dimension indicates which list this refers to. Second dimension indicates which weighting we perform (we have exactly 3 weightings in this scenario). Third level is for indicating which stone is odd (from the input). Last dimension consists of three binaries: whether the left side was lighter (moved up), whether the right side was lighter, whether both sides were equal.
Next, we make sure that we can get only one result for each weighting. This is in lines 22-29.
Next step defines another part of the model we have (lines 32-42). We need to define variables indicating which stones to put on the scale in each step. This is three dimensional array. First dimension indicates which list we have. Second dimension indicates which weighting we consider. Third dimension consists of 24 binaries: first 12 binaries indicate whether a given stone was put on the left side. Next 12 binaries do the same for the right side of the scale.
We now need to encode correctness conditions for the scale. First, we want to make sure, that we put some stones on the scale for each weighting. This is in lines 44-49. We basically take all the variables from the third dimension and make sure they are not all zeroes.
Next, we make sure that if we put a stone on the left side of the scale, then we don’t put it on the right side (and the opposite). This is in lines 51-60.
Next comes the core of the weightings. We need to calculate the result for a given list. ILP will evaluate some subset of stones to put on the scale, and we need to calculate how the scale moves. This is in lines 63-133. We iterate over every list, over every weighting, and over every instance of the input (which stone is odd and how). We then calculate some helper variables indicating whether we put more stones on one of the sides, whether this list is for checking if the stone is lighter or heavier, and whether the special stone has been put on the scale (and on which side). We then encode if conditions to make sure that the result of the weighting is stored properly.
Once we have that, we need to make sure, that our lists can actually identify the solution. We first make sure, that the algorithm we produce is deterministic. For each pair of lists, we take their prefix of ![]() steps, and if the prefixes match (so both lists tried weighting the same stones and expected the same results), then next step in both of the lists (which stones to put on the scale) must be the same. This is in lines 136-163.
steps, and if the prefixes match (so both lists tried weighting the same stones and expected the same results), then next step in both of the lists (which stones to put on the scale) must be the same. This is in lines 136-163.
Now, we need to make sure that our lists generate unique solutions. First, let’s take some list that is supposed to confirm that the third stone is lighter. We get the subsets of stones to weigh, we get the results of the weightings. We need to make sure that the result is unique, so for every other stone from the input we would get different results in weightings. This is in lines 165-.
Finally, we need to make sure that all 24 lists generate some unique weightings. If that’s the case, then we can be sure, that we get the proper algorithm for finding the odd stone. This is in lines 192-214.
We then solve the problem, and we print the solution.
Here comes some sample output:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 |
var stonesCount = 4; var weightingsCount = 3; var needToFindIfHeaverOrLigher = true; Tried aggregator 3 times. MIP Presolve eliminated 9067 rows and 4572 columns. MIP Presolve modified 33516 coefficients. Aggregator did 10560 substitutions. Reduced MIP has 24673 rows, 12164 columns, and 91360 nonzeros. Reduced MIP has 12164 binaries, 0 generals, 0 SOSs, and 0 indicators. Presolve time = 0.14 sec. (122.11 ticks) Probing time = 0.09 sec. (45.11 ticks) Tried aggregator 1 time. MIP Presolve eliminated 580 rows and 290 columns. Reduced MIP has 24093 rows, 11874 columns, and 89620 nonzeros. Reduced MIP has 11874 binaries, 0 generals, 0 SOSs, and 0 indicators. Presolve time = 0.08 sec. (63.97 ticks) Probing time = 0.13 sec. (41.80 ticks) Clique table members: 56542. MIP emphasis: balance optimality and feasibility. MIP search method: dynamic search. Parallel mode: deterministic, using up to 12 threads. Root relaxation solution time = 0.25 sec. (233.38 ticks) Nodes Cuts/ Node Left Objective IInf Best Integer Best Bound ItCnt Gap 0 0 0.0000 3549 0.0000 5007 0 0 0.0000 4634 Cuts: 3327 8757 0 0 0.0000 4153 Cuts: 3136 12012 0 0 0.0000 3716 Cuts: 4801 14696 0 0 0.0000 4840 Cuts: 2543 16843 0 2 0.0000 2182 0.0000 16843 Elapsed time = 21.00 sec. (11370.65 ticks, tree = 0.01 MB, solutions = 0) 3 5 0.0000 2182 0.0000 17507 7 9 0.0000 2843 0.0000 19561 12 14 0.0000 3079 0.0000 27692 17 19 0.0000 1784 0.0000 32431 22 24 0.0000 3615 0.0000 40876 33 35 0.0000 910 0.0000 53631 51 53 0.0000 1607 0.0000 64149 262 244 0.0000 999 0.0000 88749 271 245 0.0000 1496 0.0000 99688 359 289 0.0000 614 0.0000 134357 Elapsed time = 32.19 sec. (16729.64 ticks, tree = 2.19 MB, solutions = 0) 665 533 0.0000 813 0.0000 171436 1011 771 0.0000 1127 0.0000 198237 1441 975 infeasible 0.0000 254716 1524 971 0.0000 1466 0.0000 296856 1726 1087 infeasible 0.0000 366176 1899 1183 0.0000 1400 0.0000 406975 2235 1384 infeasible 0.0000 464046 2283 1387 0.0000 1261 0.0000 503516 2343 1395 0.0000 1740 0.0000 548927 2592 1537 0.0000 906 0.0000 600827 Elapsed time = 60.58 sec. (27170.42 ticks, tree = 27.86 MB, solutions = 0) 2882 1712 0.0000 1367 0.0000 646003 2907 1699 infeasible 0.0000 683087 2968 1676 0.0000 1964 0.0000 777718 2987 1677 0.0000 2320 0.0000 797273 3067 1701 0.0000 1557 0.0000 852616 3116 1708 0.0000 1854 0.0000 906596 3133 1725 0.0000 2004 0.0000 917695 3241 1771 0.0000 2111 0.0000 952497 3608 1922 infeasible 0.0000 1057357 3647 1893 infeasible 0.0000 1096427 Elapsed time = 97.08 sec. (39043.42 ticks, tree = 27.39 MB, solutions = 0) 3689 1893 0.0000 1526 0.0000 1141849 3703 1893 0.0000 1661 0.0000 1153728 3820 1870 0.0000 1386 0.0000 1268057 3862 1868 infeasible 0.0000 1308167 3902 1856 infeasible 0.0000 1352170 3967 1863 infeasible 0.0000 1401294 4019 1863 infeasible 0.0000 1444617 * 4162+ 1800 0.0000 0.0000 1504384 0.00% GUB cover cuts applied: 112 Clique cuts applied: 548 Cover cuts applied: 1729 Implied bound cuts applied: 5596 Mixed integer rounding cuts applied: 598 Zero-half cuts applied: 1053 Gomory fractional cuts applied: 32 Root node processing (before b&c): Real time = 20.80 sec. (11242.73 ticks) Parallel b&c, 12 threads: Real time = 99.58 sec. (35940.06 ticks) Sync time (average) = 13.62 sec. Wait time (average) = 0.00 sec. ------------ Total (root+branch&cut) = 120.38 sec. (47182.78 ticks) Stone 1 lighter: (2 ; 4) [=] ; (3 ; 4) [=] ; (1,2 ; 3,4) [>] ; Stone 1 heavier: (2 ; 4) [=] ; (3 ; 4) [=] ; (1,2 ; 3,4) [<] ; Stone 2 lighter: (2 ; 4) [>] ; (1,3 ; 2,4) [<] ; (3 ; 2) [<] ; Stone 2 heavier: (2 ; 4) [<] ; (1,3 ; 2,4) [>] ; (3,4 ; 2) [<] ; Stone 3 lighter: (2 ; 4) [=] ; (3 ; 4) [>] ; ( ; 3,4) [>] ; Stone 3 heavier: (2 ; 4) [=] ; (3 ; 4) [<] ; (1,4 ; 3) [<] ; Stone 4 lighter: (2 ; 4) [<] ; (1,3 ; 2,4) [<] ; ( ; 3) [>] ; Stone 4 heavier: (2 ; 4) [>] ; (1,3 ; 2,4) [>] ; (2 ; ) [<] ; |
Let’s see how to read that. In this simpler example, we consider 4 stones, 3 weightings, we want to find whether the odd stone is heavier or lighter. Notice, that first step in all of the lists is the same. This makes sense (we actually enforced that), because we need to have a deterministic algorithm. Pick any input instance you want to verify. Let’s say, that we assume, that the odd stone is the stone number 3, and the stone is heavier.
We take the first list from the top, and we perform the first weighting. The solution tells us to weigh stones 2 (on the left) and 4 (on the right). We weight them together. Since we know that the odd stone is the stone number 3, we know the result of this weighting will be “both sides are equal”. We see that the first list expected the result to be equal (just like second, fifth, and sixth list). Since our first list is still correct, we move to the second step of the list.
This time we need to weigh stones 3 (on the left) and 4 (on the right). We know the stone number 3 is heavier, we get the result indicated as “<" (meaning that the left side is lower than the right one). We see that the first list expects a different result. So does the second list. Third, fourth, and fifth lists expected different results in the first step. So we move to the sixth list. That list matches our results, so we move to the third step. In the third step we weigh stones 1 and 4 (on the left) with the stone number 3 (on the right). Since we have two stones on the left, the left side is heavier This is exactly what this list expects. So we know that the odd stone is the stone number 3, and that the stone is heavier (as indicated by the list). We can try other inputs. Notice, that only one list will take us through all the steps properly. Let's see another example:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
var stonesCount = 4; var weightingsCount = 2; var needToFindIfHeaverOrLigher = false; Tried aggregator 3 times. MIP Presolve eliminated 7691 rows and 3892 columns. MIP Presolve modified 21184 coefficients. Aggregator did 6560 substitutions. Reduced MIP has 13789 rows, 6780 columns, and 53032 nonzeros. Reduced MIP has 6780 binaries, 0 generals, 0 SOSs, and 0 indicators. Presolve time = 0.09 sec. (78.93 ticks) Probing time = 0.03 sec. (22.20 ticks) Tried aggregator 1 time. MIP Presolve eliminated 420 rows and 210 columns. Reduced MIP has 13369 rows, 6570 columns, and 51772 nonzeros. Reduced MIP has 6570 binaries, 0 generals, 0 SOSs, and 0 indicators. Presolve time = 0.05 sec. (37.15 ticks) Probing time = 0.06 sec. (19.96 ticks) Clique table members: 32370. MIP emphasis: balance optimality and feasibility. MIP search method: dynamic search. Parallel mode: deterministic, using up to 12 threads. Root relaxation solution time = 0.16 sec. (140.05 ticks) Nodes Cuts/ Node Left Objective IInf Best Integer Best Bound ItCnt Gap 0 0 0.0000 2081 0.0000 2874 * 0+ 0 0.0000 0.0000 4886 0.00% 0 0 cutoff 0.0000 0.0000 4886 0.00% Elapsed time = 1.92 sec. (1598.36 ticks, tree = 0.00 MB, solutions = 1) GUB cover cuts applied: 387 Clique cuts applied: 471 Cover cuts applied: 543 Implied bound cuts applied: 673 Mixed integer rounding cuts applied: 89 Zero-half cuts applied: 262 Lift and project cuts applied: 3 Gomory fractional cuts applied: 46 Root node processing (before b&c): Real time = 1.92 sec. (1598.96 ticks) Parallel b&c, 12 threads: Real time = 0.00 sec. (0.00 ticks) Sync time (average) = 0.00 sec. Wait time (average) = 0.00 sec. ------------ Total (root+branch&cut) = 1.92 sec. (1598.96 ticks) Stone 1 lighter: (1 ; 2) [>] ; (1 ; 3) [>] ; Stone 1 heavier: (1 ; 2) [<] ; (4 ; 1) [>] ; Stone 2 lighter: (1 ; 2) [<] ; (4 ; 1) [=] ; Stone 2 heavier: (1 ; 2) [>] ; (1 ; 3) [=] ; Stone 3 lighter: (1 ; 2) [=] ; (4 ; 2) [=] ; Stone 3 heavier: (1 ; 2) [=] ; (4 ; 2) [=] ; Stone 4 lighter: (1 ; 2) [=] ; (4 ; 2) [>] ; Stone 4 heavier: (1 ; 2) [=] ; (4 ; 2) [<] ; |
We have 4 stones and 2 weightings this time, but we only need to find the odd stone, without telling whether it's heavier or lighter. Let's assume once again, that our odd stone is the stone number 3, and that the stone is heavier. Let's take first step. We weigh stones 1 and 2, we get that they are equal. There are four lists that match this result. Let's take first list from the top that works for us, that is the list number 5. Second step asks us to weigh stones 4 and 2. We know these stones are equal. However, this time we have at least two lists that match this input. Those are lists 5 and 6. Both of them indicate that the odd stone is the stone number 3, but we can't tell whether the stone is lighter or heavier. Let's take another example. Again, 4 stones and 2 weightings, but this time we want to know whether the stone is heavier or lighter:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 |
var stonesCount = 4; var weightingsCount = 2; var needToFindIfHeaverOrLigher = true; Tried aggregator 3 times. MIP Presolve eliminated 7979 rows and 4028 columns. MIP Presolve modified 22428 coefficients. Aggregator did 6816 substitutions. Reduced MIP has 14617 rows, 7204 columns, and 55456 nonzeros. Reduced MIP has 7204 binaries, 0 generals, 0 SOSs, and 0 indicators. Presolve time = 0.08 sec. (81.46 ticks) Probing time = 0.05 sec. (23.52 ticks) Tried aggregator 1 time. MIP Presolve eliminated 470 rows and 235 columns. Reduced MIP has 14147 rows, 6969 columns, and 54046 nonzeros. Reduced MIP has 6969 binaries, 0 generals, 0 SOSs, and 0 indicators. Presolve time = 0.05 sec. (38.83 ticks) Probing time = 0.05 sec. (21.59 ticks) Clique table members: 33914. MIP emphasis: balance optimality and feasibility. MIP search method: dynamic search. Parallel mode: deterministic, using up to 12 threads. Root relaxation solution time = 0.16 sec. (157.25 ticks) Nodes Cuts/ Node Left Objective IInf Best Integer Best Bound ItCnt Gap 0 0 0.0000 2151 0.0000 3069 0 0 0.0000 3063 Cuts: 1847 5294 0 0 0.0000 2630 Cuts: 1606 7065 0 0 0.0000 2707 Cuts: 3502 8995 0 2 0.0000 1516 0.0000 8995 Elapsed time = 9.16 sec. (6396.65 ticks, tree = 0.01 MB, solutions = 0) 4 6 0.0000 1515 0.0000 9602 8 10 0.0000 946 0.0000 12439 9 11 0.0000 1474 0.0000 14376 16 18 0.0000 880 0.0000 24078 17 19 0.0000 1551 0.0000 25430 18 20 0.0000 2182 0.0000 28371 22 24 0.0000 1662 0.0000 33220 25 27 0.0000 2197 0.0000 37737 29 31 0.0000 950 0.0000 41055 81 77 infeasible 0.0000 82804 Elapsed time = 16.22 sec. (11603.06 ticks, tree = 0.24 MB, solutions = 0) 141 77 infeasible 0.0000 130504 207 84 0.0000 573 0.0000 171817 220 87 0.0000 1161 0.0000 181888 741 338 0.0000 502 0.0000 261716 1838 624 0.0000 511 0.0000 306384 2706 799 0.0000 473 0.0000 364713 2963 678 0.0000 968 0.0000 447687 3744 828 infeasible 0.0000 495342 4342 769 infeasible 0.0000 567069 4873 700 0.0000 749 0.0000 643508 Elapsed time = 38.22 sec. (21634.35 ticks, tree = 0.71 MB, solutions = 0) 5550 1011 0.0000 336 0.0000 688323 6408 1119 infeasible 0.0000 753821 6540 987 infeasible 0.0000 889211 6796 733 infeasible 0.0000 1027923 6887 668 infeasible 0.0000 1082863 7035 566 infeasible 0.0000 1145077 7310 401 0.0000 927 0.0000 1247273 7751 491 0.0000 1013 0.0000 1288255 8500 656 0.0000 769 0.0000 1339779 9399 708 infeasible 0.0000 1414407 Elapsed time = 61.05 sec. (31695.72 ticks, tree = 1.13 MB, solutions = 0) 9512 619 0.0000 638 0.0000 1450005 9620 548 0.0000 353 0.0000 1485033 9951 378 0.0000 1112 0.0000 1602006 10659 541 0.0000 241 0.0000 1652664 11056 602 0.0000 920 0.0000 1686445 11872 693 0.0000 899 0.0000 1743247 12902 674 infeasible 0.0000 1823367 13059 541 infeasible 0.0000 1885856 13184 450 0.0000 599 0.0000 1924334 13375 311 0.0000 1101 0.0000 1990600 Elapsed time = 85.00 sec. (42071.90 ticks, tree = 0.33 MB, solutions = 0) 13521 350 0.0000 1249 0.0000 2016520 14049 423 0.0000 987 0.0000 2064605 14529 468 0.0000 1053 0.0000 2104572 15776 529 infeasible 0.0000 2220194 15884 423 infeasible 0.0000 2273648 15975 355 0.0000 2000 0.0000 2332887 16153 353 0.0000 1040 0.0000 2400556 16231 385 0.0000 896 0.0000 2408262 16709 630 0.0000 1306 0.0000 2457290 17633 875 0.0000 1893 0.0000 2553832 Elapsed time = 110.98 sec. (53742.88 ticks, tree = 0.69 MB, solutions = 0) 17655 887 0.0000 2059 0.0000 2572045 17739 925 0.0000 2061 0.0000 2592268 18467 1245 infeasible 0.0000 2809240 18490 1222 infeasible 0.0000 2862765 18509 1203 infeasible 0.0000 2894288 18538 1174 infeasible 0.0000 2954243 18550 1162 infeasible 0.0000 2977278 18603 1111 infeasible 0.0000 3071110 18632 1082 infeasible 0.0000 3113050 18657 1057 infeasible 0.0000 3152949 Elapsed time = 139.20 sec. (65489.88 ticks, tree = 1.02 MB, solutions = 0) 18703 1035 0.0000 1538 0.0000 3215507 18766 992 0.0000 1513 0.0000 3289399 18773 991 0.0000 1954 0.0000 3299613 18785 987 0.0000 1870 0.0000 3317451 18810 968 infeasible 0.0000 3353816 18937 848 0.0000 1405 0.0000 3504999 18945 840 infeasible 0.0000 3513374 19002 807 0.0000 1521 0.0000 3552254 19027 788 0.0000 889 0.0000 3567473 19074 757 0.0000 1516 0.0000 3598113 Elapsed time = 174.28 sec. (78644.14 ticks, tree = 0.72 MB, solutions = 0) 19209 688 0.0000 1421 0.0000 3671212 19576 636 0.0000 1336 0.0000 3793448 19876 730 0.0000 1286 0.0000 3830126 20633 786 0.0000 1087 0.0000 3919803 20698 783 0.0000 1761 -0.0000 3938066 20701 783 0.0000 1772 -0.0000 3939038 20706 784 0.0000 1737 -0.0000 3941101 20712 785 0.0000 1527 -0.0000 3943797 20723 792 0.0000 1686 -0.0000 3948083 20744 802 0.0000 1368 -0.0000 3960461 Elapsed time = 214.22 sec. (104503.67 ticks, tree = 7.09 MB, solutions = 0) 20836 823 0.0000 1726 -0.0000 3986141 21274 760 0.0000 802 -0.0000 4028859 22072 706 0.0000 555 -0.0000 4079944 22658 913 0.0000 587 -0.0000 4118471 23413 1131 0.0000 638 -0.0000 4165697 24085 1269 0.0000 1102 -0.0000 4208939 24697 1362 0.0000 1467 -0.0000 4249456 24707 1364 0.0000 1395 -0.0000 4250658 24823 1048 0.0000 1095 -0.0000 4257228 25065 1071 infeasible -0.0000 4300075 Elapsed time = 239.13 sec. (123018.58 ticks, tree = 13.01 MB, solutions = 0) 25299 1026 0.0000 1528 -0.0000 4346987 25703 880 0.0000 1260 -0.0000 4413791 25956 726 0.0000 1484 -0.0000 4464113 26326 642 infeasible -0.0000 4531938 26709 764 0.0000 1392 -0.0000 4600736 27194 830 0.0000 1504 -0.0000 4690663 27505 881 infeasible -0.0000 4754242 27728 910 0.0000 1401 -0.0000 4805393 28143 972 infeasible -0.0000 4890255 29468 1242 0.0000 1129 -0.0000 5156954 Elapsed time = 268.17 sec. (135740.89 ticks, tree = 0.72 MB, solutions = 0) 30823 1629 0.0000 1514 -0.0000 5412126 32350 1829 infeasible -0.0000 5718157 33681 2055 0.0000 1806 -0.0000 5982692 35083 2390 0.0000 1073 -0.0000 6250237 36581 2505 0.0000 1043 -0.0000 6529869 37841 2625 infeasible -0.0000 6817490 39098 2867 infeasible -0.0000 7048531 40747 3107 infeasible -0.0000 7290962 42603 3141 0.0000 1660 -0.0000 7563118 44182 3230 infeasible -0.0000 7819515 Elapsed time = 361.98 sec. (174394.28 ticks, tree = 4.79 MB, solutions = 0) 45619 3223 infeasible -0.0000 8097725 46934 3130 0.0000 1454 -0.0000 8347398 48243 3130 infeasible -0.0000 8596902 49646 3295 0.0000 1690 -0.0000 8877792 51457 3485 0.0000 1713 -0.0000 9148822 53014 3570 infeasible -0.0000 9418591 54081 3625 0.0000 1030 -0.0000 9606215 55525 3715 0.0000 1189 -0.0000 9877402 56700 3928 0.0000 855 -0.0000 10075168 58063 4056 infeasible -0.0000 10333360 Elapsed time = 456.38 sec. (212954.00 ticks, tree = 10.13 MB, solutions = 0) 59500 4151 0.0000 1234 -0.0000 10584348 60939 4343 infeasible -0.0000 10827749 62208 4431 0.0000 936 -0.0000 11070122 63869 4520 infeasible -0.0000 11332455 65291 4460 infeasible -0.0000 11588607 66927 4504 infeasible -0.0000 11858213 67955 4528 0.0000 1910 -0.0000 12076043 69355 4604 infeasible -0.0000 12348814 70699 4650 infeasible -0.0000 12610568 71789 4734 0.0000 1329 -0.0000 12800946 Elapsed time = 545.30 sec. (251434.93 ticks, tree = 13.54 MB, solutions = 0) 73016 4916 0.0000 1487 -0.0000 13037540 74506 5023 infeasible -0.0000 13269173 76094 5090 infeasible -0.0000 13528840 77625 5202 0.0000 1735 -0.0000 13792072 78726 5106 infeasible -0.0000 14003840 79889 5084 infeasible -0.0000 14231445 81320 5038 infeasible -0.0000 14505353 82040 4900 infeasible -0.0000 14661949 83548 4972 0.0000 1589 -0.0000 14955703 84626 4843 infeasible -0.0000 15167841 Elapsed time = 632.33 sec. (290030.55 ticks, tree = 14.75 MB, solutions = 0) 86294 5088 infeasible -0.0000 15387594 87804 5225 0.0000 1359 -0.0000 15564328 88886 5244 infeasible -0.0000 15699728 90552 5271 infeasible -0.0000 15948314 91964 5264 infeasible -0.0000 16180305 93433 5389 infeasible -0.0000 16427669 94565 5307 0.0000 1120 -0.0000 16621300 95994 5212 0.0000 1455 -0.0000 16873270 97427 5247 infeasible -0.0000 17129972 98889 5287 0.0000 983 -0.0000 17406516 Elapsed time = 719.33 sec. (328416.41 ticks, tree = 27.38 MB, solutions = 0) 99907 5228 0.0000 1328 -0.0000 17575397 101302 5330 infeasible -0.0000 17823322 102799 5214 0.0000 863 -0.0000 18099640 103764 5170 0.0000 1129 -0.0000 18285881 105271 5249 0.0000 1271 -0.0000 18554404 106449 5160 0.0000 1543 -0.0000 18755055 107926 5113 0.0000 1762 -0.0000 19016073 108946 5142 infeasible -0.0000 19221112 110335 5099 0.0000 777 -0.0000 19481823 111545 4980 0.0000 1704 -0.0000 19710912 Elapsed time = 805.23 sec. (366844.78 ticks, tree = 23.88 MB, solutions = 0) 112585 4819 0.0000 1424 -0.0000 19941208 113784 4892 0.0000 1509 -0.0000 20193029 114777 4798 infeasible -0.0000 20389392 116492 4784 infeasible -0.0000 20686235 117583 4572 infeasible -0.0000 20908289 118640 4660 0.0000 970 -0.0000 21116568 119860 4641 infeasible -0.0000 21355030 121382 4590 0.0000 1454 -0.0000 21627839 122351 4608 0.0000 1265 -0.0000 21797169 123588 4526 0.0000 1700 -0.0000 22052286 Elapsed time = 893.16 sec. (405404.89 ticks, tree = 19.45 MB, solutions = 0) 124597 4542 0.0000 1581 -0.0000 22246731 125830 4603 0.0000 1411 -0.0000 22485436 127235 4523 0.0000 1640 -0.0000 22742415 128168 4478 0.0000 1636 -0.0000 22911720 129565 4484 0.0000 1000 -0.0000 23181009 130743 4487 0.0000 1599 -0.0000 23351196 132108 4479 0.0000 1378 -0.0000 23550263 133548 4330 infeasible -0.0000 23826937 134461 4260 0.0000 1144 -0.0000 24037776 135337 4300 0.0000 1185 -0.0000 24239681 Elapsed time = 980.72 sec. (444203.37 ticks, tree = 20.49 MB, solutions = 0) 136369 4298 0.0000 1345 -0.0000 24438674 137776 4279 infeasible -0.0000 24669845 138913 4133 0.0000 1142 -0.0000 24923243 139683 4024 0.0000 1013 -0.0000 25089334 140779 4056 0.0000 1273 -0.0000 25275702 142463 4028 0.0000 1275 -0.0000 25559396 143596 4029 0.0000 1421 -0.0000 25801485 144449 4108 0.0000 1474 -0.0000 25999187 145595 4199 0.0000 1814 -0.0000 26236291 146576 4192 infeasible -0.0000 26430551 Elapsed time = 1068.33 sec. (482851.65 ticks, tree = 23.50 MB, solutions = 0) 147814 4325 0.0000 1747 -0.0000 26660597 149075 4345 0.0000 1244 -0.0000 26937802 150223 4396 infeasible -0.0000 27146886 151396 4372 0.0000 1272 -0.0000 27326098 152752 4293 0.0000 1545 -0.0000 27564920 153548 4127 0.0000 1268 -0.0000 27771342 154765 4064 0.0000 1057 -0.0000 27981568 155488 3955 infeasible -0.0000 28150713 156418 3765 infeasible -0.0000 28383049 157341 3595 0.0000 1666 -0.0000 28576333 Elapsed time = 1152.84 sec. (521275.28 ticks, tree = 22.79 MB, solutions = 0) 158467 3589 0.0000 1136 -0.0000 28815572 159532 3561 0.0000 1803 -0.0000 29040318 160465 3611 0.0000 1598 -0.0000 29279594 161411 3625 infeasible -0.0000 29511805 162031 3578 0.0000 832 -0.0000 29642435 163258 3549 0.0000 919 -0.0000 29941674 163927 3560 0.0000 1921 -0.0000 30088371 165262 3556 0.0000 1464 -0.0000 30381954 166573 3540 infeasible -0.0000 30624650 167811 3509 0.0000 1489 -0.0000 30890814 Elapsed time = 1243.14 sec. (559789.31 ticks, tree = 16.68 MB, solutions = 0) 168651 3427 infeasible -0.0000 31073463 170018 3445 infeasible -0.0000 31286141 170741 3286 0.0000 1484 -0.0000 31424810 172175 3297 infeasible -0.0000 31707599 172965 3208 0.0000 1736 -0.0000 31868977 174150 3090 infeasible -0.0000 32138345 175160 3044 0.0000 1107 -0.0000 32355657 175994 2990 0.0000 1593 -0.0000 32555554 177147 2771 infeasible -0.0000 32778058 178088 2697 0.0000 1883 -0.0000 32977587 Elapsed time = 1330.00 sec. (598388.63 ticks, tree = 5.88 MB, solutions = 0) 178865 2623 0.0000 1670 -0.0000 33186397 179659 2568 infeasible -0.0000 33347250 180686 2520 infeasible -0.0000 33607419 181816 2384 0.0000 1800 -0.0000 33867732 182642 2300 infeasible -0.0000 34051617 183672 2248 0.0000 1716 -0.0000 34251822 184628 2049 0.0000 1881 -0.0000 34486471 185359 1843 0.0000 917 -0.0000 34650208 186210 1758 0.0000 1685 -0.0000 34883935 186808 1625 infeasible -0.0000 35060248 Elapsed time = 1418.44 sec. (637045.35 ticks, tree = 2.74 MB, solutions = 0) 187666 1390 0.0000 1656 -0.0000 35284509 188282 1348 0.0000 1607 -0.0000 35454477 188974 1294 infeasible -0.0000 35658533 189819 1284 0.0000 1344 -0.0000 35878470 190530 1111 0.0000 1847 -0.0000 36069288 191306 1126 0.0000 1961 -0.0000 36238662 192172 1193 infeasible -0.0000 36457694 192817 1169 0.0000 1389 -0.0000 36644583 193478 1202 0.0000 408 -0.0000 36869749 194158 1161 0.0000 1825 -0.0000 37060379 Elapsed time = 1506.59 sec. (676153.52 ticks, tree = 2.70 MB, solutions = 0) 194823 1047 infeasible -0.0000 37314861 195274 902 0.0000 2100 -0.0000 37464452 195909 731 0.0000 1760 -0.0000 37659892 196478 737 infeasible -0.0000 37804184 197079 644 infeasible -0.0000 38034960 197760 600 0.0000 1947 -0.0000 38279954 198275 538 0.0000 2168 -0.0000 38437348 198876 476 infeasible -0.0000 38643813 199376 406 infeasible -0.0000 38820484 200186 333 0.0000 2000 -0.0000 38993643 Elapsed time = 1593.83 sec. (714834.63 ticks, tree = 0.36 MB, solutions = 0) 200819 171 infeasible -0.0000 39193590 201410 67 infeasible -0.0000 39359622 201695 1 infeasible -0.0000 39435653 Root node processing (before b&c): Real time = 9.05 sec. (6330.63 ticks) Parallel b&c, 12 threads: Real time = 1610.13 sec. (720154.57 ticks) Sync time (average) = 172.85 sec. Wait time (average) = 0.07 sec. ------------ Total (root+branch&cut) = 1619.17 sec. (726485.20 ticks) Stone 1 lighter: ILOG.CPLEX.CpxException: CPLEX Error 1217: No solution exists. at ILOG.CPLEX.CplexI.CALL(Int32 status) at ILOG.CPLEX.CplexI.GetXcache() at ILOG.CPLEX.Cplex.GetValue(INumExpr expr) at CplexMilpManager.Implementation.CplexMilpSolver.GetValue(IVariable variable) in C:\Users\afish\Desktop\milpmanager\CplexMilpSolver\Implementation\CplexMilpSolver.cs:line 160 at IlpPlayground.Program420502851.<>c__DisplayClass18.<Start>b__8(Int32 stoneId) at System.Linq.Enumerable.WhereSelectEnumerableIterator`2.MoveNext() at System.Linq.Enumerable.WhereSelectEnumerableIterator`2.MoveNext() at System.String.Join[T](String separator, IEnumerable`1 values) at IlpPlayground.Program420502851.Start() at IlpPlayground.Env420502851.Start() |
CPLEX indicates there are no solutions. This makes sense, we can't tell the solution for sure with 2 weightings only. Here comes the solution for 12 stones and 3 moves:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
Stone 1 lighter: (1,2,3,4 ; 5,6,7,8) [>] ; (3,4,5,6 ; 1,8,9,10) [<] ; (5 ; 6) [=] ; Stone 1 heavier: (1,2,3,4 ; 5,6,7,8) [<] ; (4,5,9,10 ; 1,2,7,8) [>] ; (1 ; 2) [<] ; Stone 2 lighter: (1,2,3,4 ; 5,6,7,8) [>] ; (3,4,5,6 ; 1,8,9,10) [=] ; (11 ; 2) [<] ; Stone 2 heavier: (1,2,3,4 ; 5,6,7,8) [<] ; (4,5,9,10 ; 1,2,7,8) [>] ; (1 ; 2) [>] ; Stone 3 lighter: (1,2,3,4 ; 5,6,7,8) [>] ; (3,4,5,6 ; 1,8,9,10) [>] ; (3 ; 4) [>] ; Stone 3 heavier: (1,2,3,4 ; 5,6,7,8) [<] ; (4,5,9,10 ; 1,2,7,8) [=] ; (11 ; 3) [>] ; Stone 4 lighter: (1,2,3,4 ; 5,6,7,8) [>] ; (3,4,5,6 ; 1,8,9,10) [>] ; (3 ; 4) [<] ; Stone 4 heavier: (1,2,3,4 ; 5,6,7,8) [<] ; (4,5,9,10 ; 1,2,7,8) [<] ; (7 ; 8) [=] ; Stone 5 lighter: (1,2,3,4 ; 5,6,7,8) [<] ; (4,5,9,10 ; 1,2,7,8) [>] ; (1 ; 2) [=] ; Stone 5 heavier: (1,2,3,4 ; 5,6,7,8) [>] ; (3,4,5,6 ; 1,8,9,10) [<] ; (5 ; 6) [<] ; Stone 6 lighter: (1,2,3,4 ; 5,6,7,8) [<] ; (4,5,9,10 ; 1,2,7,8) [=] ; (11 ; 3) [=] ; Stone 6 heavier: (1,2,3,4 ; 5,6,7,8) [>] ; (3,4,5,6 ; 1,8,9,10) [<] ; (5 ; 6) [>] ; Stone 7 lighter: (1,2,3,4 ; 5,6,7,8) [<] ; (4,5,9,10 ; 1,2,7,8) [<] ; (7 ; 8) [>] ; Stone 7 heavier: (1,2,3,4 ; 5,6,7,8) [>] ; (3,4,5,6 ; 1,8,9,10) [=] ; (11 ; 2) [=] ; Stone 8 lighter: (1,2,3,4 ; 5,6,7,8) [<] ; (4,5,9,10 ; 1,2,7,8) [<] ; (7 ; 8) [<] ; Stone 8 heavier: (1,2,3,4 ; 5,6,7,8) [>] ; (3,4,5,6 ; 1,8,9,10) [>] ; (3 ; 4) [=] ; Stone 9 lighter: (1,2,3,4 ; 5,6,7,8) [=] ; (1,2,3 ; 9,10,11) [<] ; (9 ; 10) [>] ; Stone 9 heavier: (1,2,3,4 ; 5,6,7,8) [=] ; (1,2,3 ; 9,10,11) [>] ; (9 ; 10) [<] ; Stone 10 lighter: (1,2,3,4 ; 5,6,7,8) [=] ; (1,2,3 ; 9,10,11) [<] ; (9 ; 10) [<] ; Stone 10 heavier: (1,2,3,4 ; 5,6,7,8) [=] ; (1,2,3 ; 9,10,11) [>] ; (9 ; 10) [>] ; Stone 11 lighter: (1,2,3,4 ; 5,6,7,8) [=] ; (1,2,3 ; 9,10,11) [<] ; (9 ; 10) [=] ; Stone 11 heavier: (1,2,3,4 ; 5,6,7,8) [=] ; (1,2,3 ; 9,10,11) [>] ; (9 ; 10) [=] ; Stone 12 lighter: (1,2,3,4 ; 5,6,7,8) [=] ; (1,2,3 ; 9,10,11) [=] ; (1 ; 12) [<] ; Stone 12 heavier: (1,2,3,4 ; 5,6,7,8) [=] ; (1,2,3 ; 9,10,11) [=] ; (1 ; 12) [>] ; |
Big thanks to Tomasz Masternak. We had lots of fun discussing the problem.