This is the eightieth first part of the ILP series. For your convenience you can find other parts in the table of contents in Part 1 – Boolean algebra
Today we are going to solve Kakuro:
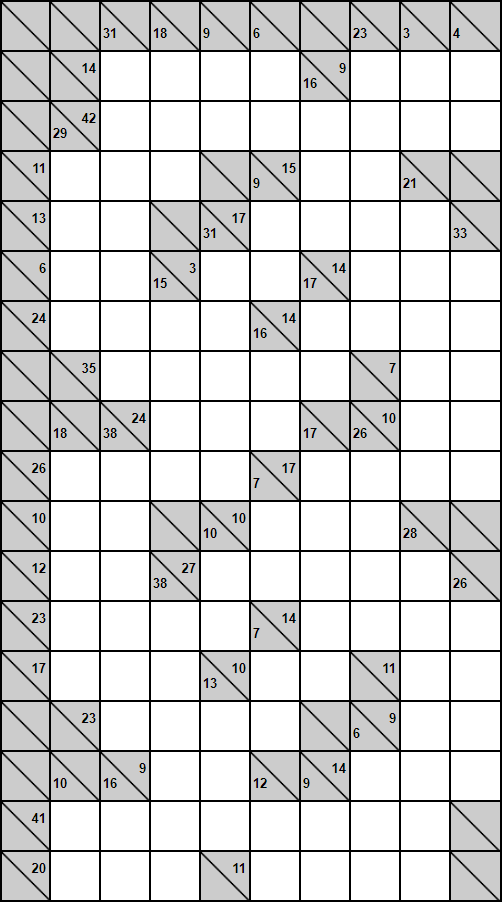
Code:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 |
var rows = new int[][]{ new int[]{0,0,0,0,0,0,0,0,0,0}, new int[]{0,0,1,1,1,1,0,2,2,2}, new int[]{0,0,3,3,3,3,3,3,3,3}, new int[]{0,4,4,4,0,0,5,5,0,0}, new int[]{0,6,6,0,0,7,7,7,7,0}, new int[]{0,8,8,0,9,9,0,10,10,10}, new int[]{0,11,11,11,11,0,12,12,12,12}, new int[]{0,0,13,13,13,13,13,0,14,14}, new int[]{0,0,0,15,15,15,0,0,16,16}, new int[]{0,17,17,17,17,0,18,18,18,18}, new int[]{0,19,19,0,0,20,20,20,0,0}, new int[]{0,21,21,0,22,22,22,22,22,0}, new int[]{0,23,23,23,23,0,24,24,24,24}, new int[]{0,25,25,25,0,26,26,0,27,27}, new int[]{0,0,28,28,28,28,0,0,29,29}, new int[]{0,0,0,30,30,0,0,31,31,31}, new int[]{0,32,32,32,32,32,32,32,32,0}, new int[]{0,33,33,33,0,34,34,34,34,0} }; var rowPoints = new Dictionary<int, int>(){ {1, 14}, {2, 9}, {3, 42}, {4, 11}, {5, 15}, {6, 13}, {7, 17}, {8, 6}, {9, 3}, {10, 14}, {11, 24}, {12, 14}, {13, 35}, {14, 7}, {15, 24}, {16, 10}, {17, 26}, {18, 17}, {19, 10}, {20, 10}, {21, 12}, {22, 27}, {23, 23}, {24, 14}, {25, 17}, {26, 10}, {27, 11}, {28, 23}, {29, 9}, {30, 9}, {31, 14}, {32, 41}, {33, 20}, {34, 11} }; var columns = new int[][]{ new int[]{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0}, new int[]{0,0,0,1,1,1,1,0,0,2,2,2,2,2,0,0,3,3}, new int[]{0,4,4,4,4,4,4,4,0,5,5,5,5,5,5,0,6,6}, new int[]{0,7,7,7,0,0,8,8,8,8,0,0,9,9,9,9,9,9}, new int[]{0,10,10,0,0,11,11,11,11,11,0,12,12,0,13,13,13,0}, new int[]{0,14,14,0,15,15,0,16,16,0,17,17,0,18,18,0,19,19}, new int[]{0,0,20,20,20,0,21,21,0,22,22,22,22,22,0,0,23,23}, new int[]{0,24,24,24,24,24,24,0,0,25,25,25,25,0,0,26,26,26}, new int[]{0,27,27,0,28,28,28,28,28,28,0,29,29,29,29,29,29,29}, new int[]{0,30,30,0,0,31,31,31,31,31,0,0,32,32,32,32,0,0} }; var columnPoints = new Dictionary<int, int>(){ {1, 29}, {2, 18}, {3, 10}, {4, 31}, {5, 38}, {6, 16}, {7, 18}, {8, 15}, {9, 38}, {10, 9}, {11, 31}, {12, 10}, {13, 13}, {14, 6}, {15, 9}, {16, 16}, {17, 7}, {18, 7}, {19, 12}, {20, 16}, {21, 17}, {22, 17}, {23, 9}, {24, 23}, {25, 26}, {26, 6}, {27, 3}, {28, 21}, {29, 28}, {30, 4}, {31, 33}, {32, 26} }; var variables = Enumerable.Range(0, rows.Length).Select(r => Enumerable.Range(0, rows[r].Length).Select(c => solver.CreateAnonymous(Domain.PositiveOrZeroInteger)).ToArray()).ToArray(); foreach(var v in variables.SelectMany(r => r)){ v.Set<LessOrEqual>(solver.FromConstant(9)); } foreach(var p in rowPoints){ var key = p.Key; var sum = p.Value; List<IVariable> vars = new List<IVariable>(); for(int i=0;i<rows.Length;++i){ for(int j=0;j<rows[0].Length;++j){ if(rows[i][j] == key){ vars.Add(variables[i][j]); } } } solver.Operation<Addition>(vars.ToArray()).Set<Equal>(solver.FromConstant(sum)); solver.Set<AllDifferent>(solver.FromConstant(0), vars.ToArray()); }; foreach(var p in columnPoints){ var key = p.Key; var sum = p.Value; List<IVariable> vars = new List<IVariable>(); for(int i=0;i<columns.Length;++i){ for(int j=0;j<columns[0].Length;++j){ if(columns[i][j] == key){ vars.Add(variables[j][i]); } } } solver.Operation<Addition>(vars.ToArray()).Set<Equal>(solver.FromConstant(sum)); solver.Set<AllDifferent>(solver.FromConstant(0), vars.ToArray()); }; solver.AddGoal("g", solver.FromConstant(0)); solver.Solve(); for(int i=0;i<rows.Length;++i){ for(int j=0;j<rows[0].Length;++j){ Console.Write(solver.GetValue(variables[i][j])); } Console.WriteLine(); } |
Should be self explanatory now. Solution:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 |
Tried aggregator 3 times. MIP Presolve eliminated 3334 rows and 1776 columns. MIP Presolve modified 7505 coefficients. Aggregator did 32 substitutions. Reduced MIP has 1682 rows, 740 columns, and 4680 nonzeros. Reduced MIP has 652 binaries, 88 generals, 0 SOSs, and 0 indicators. Presolve time = 0.01 sec. (9.86 ticks) Probing fixed 105 vars, tightened 93 bounds. Probing changed sense of 275 constraints. Probing time = 0.02 sec. (6.33 ticks) Cover probing fixed 0 vars, tightened 98 bounds. Tried aggregator 2 times. MIP Presolve eliminated 421 rows and 207 columns. MIP Presolve modified 982 coefficients. Aggregator did 185 substitutions. Reduced MIP has 1076 rows, 348 columns, and 3219 nonzeros. Reduced MIP has 265 binaries, 83 generals, 0 SOSs, and 0 indicators. Presolve time = 0.00 sec. (5.22 ticks) Probing fixed 5 vars, tightened 9 bounds. Probing time = 0.00 sec. (1.53 ticks) Tried aggregator 1 time. MIP Presolve eliminated 19 rows and 5 columns. MIP Presolve modified 120 coefficients. Reduced MIP has 1057 rows, 343 columns, and 3165 nonzeros. Reduced MIP has 260 binaries, 83 generals, 0 SOSs, and 0 indicators. Presolve time = 0.00 sec. (1.54 ticks) Probing fixed 4 vars, tightened 10 bounds. Probing time = 0.00 sec. (1.49 ticks) Clique table members: 688. MIP emphasis: balance optimality and feasibility. MIP search method: dynamic search. Parallel mode: deterministic, using up to 8 threads. Root relaxation solution time = 0.02 sec. (7.98 ticks) Nodes Cuts/ Node Left Objective IInf Best Integer Best Bound ItCnt Gap 0 0 0.0000 65 0.0000 215 0 0 0.0000 30 Cuts: 60 271 0 0 0.0000 102 Cuts: 115 375 0 0 0.0000 35 Cuts: 20 393 0 0 0.0000 48 Cuts: 48 443 * 0+ 0 0.0000 0.0000 443 0.00% 0 0 cutoff 0.0000 0.0000 443 0.00% Elapsed time = 0.36 sec. (133.69 ticks, tree = 0.00 MB, solutions = 1) Clique cuts applied: 10 Cover cuts applied: 1 Implied bound cuts applied: 22 Flow cuts applied: 1 Mixed integer rounding cuts applied: 8 Zero-half cuts applied: 25 Gomory fractional cuts applied: 3 Root node processing (before b&c): Real time = 0.38 sec. (133.77 ticks) Parallel b&c, 8 threads: Real time = 0.00 sec. (0.00 ticks) Sync time (average) = 0.00 sec. Wait time (average) = 0.00 sec. ------------ Total (root+branch&cut) = 0.38 sec. (133.77 ticks) 0000000000 0028310513 0079658421 0731007800 0940071360 0510120248 0861908123 0085679016 0007890037 0892701259 0370012700 0480164970 0158903812 0269037038 0037940027 0006300149 0275198360 0893031250 |