This is the forty thrid part of the ILP series. For your convenience you can find other parts in the table of contents in Part 1 – Boolean algebra
We have already seen how to implement ![]() function in ILP. Last time we used comparisons, today we will perform bit operations.
function in ILP. Last time we used comparisons, today we will perform bit operations.
Idea
Having non-negative variables ![]() and
and ![]() we want to calculate
we want to calculate ![]() . First, we decompose variables into its binary representation as in multiplication. Nest, we use the following trick: if
. First, we decompose variables into its binary representation as in multiplication. Nest, we use the following trick: if ![]() then there must be a n index
then there must be a n index ![]() for which
for which ![]() is one and
is one and ![]() is zero.
is zero.
Proof: let’s assume that ![]() which means that
which means that ![]() , and there is no index for which
, and there is no index for which ![]() and
and ![]() . At the same time
. At the same time ![]() . But since there is no index we want to find, each
. But since there is no index we want to find, each ![]() is not greater than zero. So the whole sum is not greater than zero — contradiction.
is not greater than zero. So the whole sum is not greater than zero — contradiction.
Now we only need to find this index.
Finding index
We will simply bruteforce index. For each position we define the following variables:
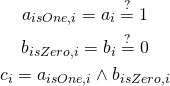
Now, ![]() is desired index if and only if
is desired index if and only if ![]() is one and all
is one and all ![]() for
for ![]() is zero:
is zero:
![]()
The only missing bit:
![]()
Now we can perform multiplication to select maximum value using calculated flag.