This is the thirty eighth part of the ILP series. For your convenience you can find other parts in the table of contents in Part 1 – Boolean algebra
Today we are going to implement basic data structure: array. If you know functional programming and immutable data structures, you will find this post as almost direct implementation of that concepts.
Table of Contents
Idea
Let’s begin with explaining what an array is. In our case this is simply a zero-based vector of variables. Having such a vector we can extract element with specified index, or set value at specified index. Our array is static — it will not expand dynamically. We are also not going to cover bound checks, we assume that we use correct indexes.
More formally, we have the following array:
![]()
We can extract element:
![]()
We can also set element:
![]()
Extracting element
In order to get element we could use simple conditions:
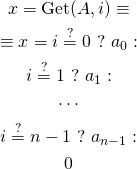
We compare index with consecutive values and extract matching value from the array. If we cannot match the index — we return zero (or any other default value).
However, this is a bit slow. In theory we could implement binary search to match the index, but for now let’s stick to linear search.
However, instead of using conditions, we can simulate them in binary logic. Key idea here is: if we define result value (![]() in our case), we can construct constraint saying that
in our case), we can construct constraint saying that ![]() must be equal to some value when index matches position in element. Crazy, huh? Formula is:
must be equal to some value when index matches position in element. Crazy, huh? Formula is:
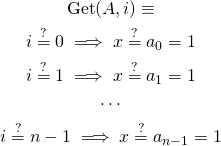
How does it work? If ![]() is not zero, left side of implication is false. This means, that whole implication is true (remember logic tables?), so this constraints changes nothing. We move on to next value. When we come to the right value, which means that
is not zero, left side of implication is false. This means, that whole implication is true (remember logic tables?), so this constraints changes nothing. We move on to next value. When we come to the right value, which means that ![]() is equal to some specified index, left side of implication is true. Since we require whole implication to hold, its right side must be true as well — this means, that
is equal to some specified index, left side of implication is true. Since we require whole implication to hold, its right side must be true as well — this means, that ![]() will get value of
will get value of ![]() . We still compare values but we don’t need to calculate condition operation which is quite heavy.
. We still compare values but we don’t need to calculate condition operation which is quite heavy.
Please also note, that this has unspecified behavior when index doesn’t point to any correct index — previous approach returned default value in that case, this time ![]() can be simply anything.
can be simply anything.
Setting element
This part is a bit harder — in theory any element can be modified, so we need to update all of them:
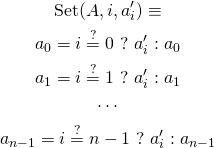
Summary
This is whole implementation. Extraction takes linear time, changing element takes linear time as well. However, please note that this structure can be easily transformed into dictionary. Next time we will see how to utilize array to implement nondeterministic Turing machine in ILP. Stay tuned.