This is the twenty seventh part of the ILP series. For your convenience you can find other parts in the table of contents in Part 1 – Boolean algebra
Hi! Today we are going to solve Einstein’s five houses riddle using ILP!
Table of Contents
Introduction
In the riddle we have five houses. Person living in every house can be described using five traits (nationality, favorite drink, spoked stuff, color of the house, and favorite pet). For every trait we have five different values: there are five colors, five animals, five drinks etc. We are given some logical constraints describing the persons and wee need to find the final matching between houses and traits. Looks like ideal case for our ILP program!
Matrix of traits
We have the following traits:
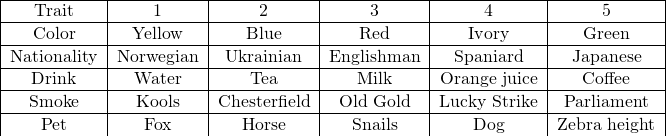
We define the following binary variables:
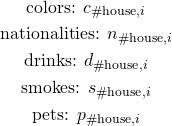
Every variable answers the question if the associated house has the associated trait set to true. For instance, ![]() set to true means that the house number
set to true means that the house number ![]() is blue, whereas
is blue, whereas ![]() would mean that the guy living in house number
would mean that the guy living in house number ![]() smokes Kools.
smokes Kools.
Constraints
We need to add basic constraints that one trait is associated with exactly one house:
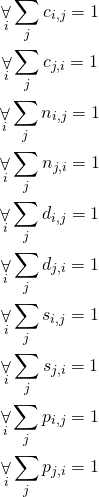
Now we can add formulas for constraints specified in the riddle.
The Englishman lives in the red house.
![]()
The Spaniard owns the dog.
![]()
Coffee is drunk in the green house.
![]()
The Ukrainian drinks tea.
![]()
The green house is immediately to the right of the ivory house.
![]()
The Old Gold smoker owns snails.
![]()
Kools are smoked in the yellow house.
![]()
Milk is drunk in the middle house.
![]()
The Norwegian lives in the first house.
![]()
The man who smokes Chesterfields lives in the house next to the man with the fox.
![]()
Kools are smoked in the house next to the house where the horse is kept.
![]()
The Lucky Strike smoker drinks orange juice.
![]()
The Japanese smokes Parliaments.
![]()
The Norwegian lives next to the blue house.
![]()
Summary
As we can see it is very easy to solve the Einstein’s riddle using ILP. Most of the constraints are straightforward, only constraints of type “something is in the house next to” are a bit more difficult.