This is the twenty first part of the ILP series. For your convenience you can find other parts in the table of contents in Part 1 – Boolean algebra
So far, we have defined constraints which make our final solution “feasible”. The students will likely not be very happy with their schedules, but they will at least be able to attend all the classes they want to. It is time to find a way to make them happy.
Table of Contents
Introduction
There is a question — what does it mean to be “happy”? As we will shortly see, there are at least few ways to calculate the level of happiness and each of them gives different results. It is not easy to compare two solutions because we always need to remember that even an optimal solution does not mean that students are completely happy, because it depends on the method of calculating happiness.
Before we describe the methods of calculating happiness, we need to consider a few details of preference points. Every student can make his decision by distributing preference points for classes in the courses. We assume, that the student cannot have more than ![]() preferences points in a single course—which means, that
preferences points in a single course—which means, that  . This also means that most of the students’ wishes
. This also means that most of the students’ wishes ![]() will be equal to
will be equal to ![]() .
.
Sum of Preference Points
The simplest method of calculating happiness is by adding all the gained preference points. As we have defined in Section~??, when variable ![]() is equal to
is equal to ![]() , we say that student
, we say that student ![]() gained points for his wish for class
gained points for his wish for class ![]() . We define our goal function as a sum of all these points:
. We define our goal function as a sum of all these points:
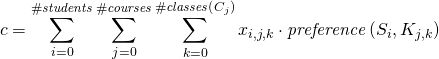
By maximizing this function, we increase the total happiness of students, because the solver will try to assign them to classes they want to be assigned to. This is called the “Utilitarian Approach”.
Let us consider advantages and disadvantages of this approach. This formula is easy in implementation and can be calculated very quickly. Perhaps even more importantly, it is rather easy to answer the question how should students distribute their preference points”, because the total value of the cost function is simply the sum of students’ preferences. So when two students decide to give preference points for a particular class, we can suspect that the student who gave more preference points for that class will be assigned to it. This is an advantage and a disadvantage at the same time.
Let us consider two students, who are registered for calculus exercises. Imagine that student A gave 10 points for class C, and student B gave 5 points for that class. In an isolated case, when there is the last place left in class C, the solver should assign student A, because he gave 10 points, so he will increase the cost function by 10, whereas student B would increase it only by 5. Let us assume that student B gave no more than 5 points for any of the classes. In this distribution of points, he is in worse position (from the solver’s point of view), because he cannot increase the cost function by more than 5 points from one class, so in direct confrontation with student A he will always lose. However, placing student B in that class would mean giving him his most wanted class (because it is his highest preference points decision).
Whether this situation is advantageous or disadvantageous cannot be simply answered. It is a matter of choice or particular needs. Let us now consider different methods of calculating happiness, which do not suffer from this confrontation effect.
Sum of Preferences per Student
This method is very similar to the previous one. We once again sum all of the preference points, but before summing them, we divide them by the maximum amount of the preference points which students can gain.
To explain this, let us consider an example. Imagine that calculus course has two classes: class M (which happens on Monday) and class F (which happens on Friday). We have two students: student A gives 5 points for class M and 3 points for class F, student B gives 10 points for class M and 8 points for class F. We need to assign each of them to exactly one class of calculus per week, which means, that every student will be assigned to class M or to class F, and not to both of them. In this case, the total number of points which student A can gain is 5, because he can gain 5 points for class M or 3 points for class F, and he cannot gain more. Student B can gain at most 10 points for his wish for class M.
To calculate the cost function, we sum the students’ gained preference points, but we divide them by the total amount of points they can gain for all their courses. In our example, we divide student A’s points by 5, and student’s B points by 10. Let us denote the total possible amount of points which student ![]() can gain as
can gain as ![]() , the general cost function formula is as follows:
, the general cost function formula is as follows:
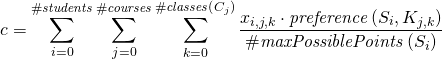
With this approach we treat students’ preferences as their relative needs. ![]() points no longer means the most wanted class, student can indicate that, for instance, all of the classes are equally desired (by giving the same amount of points to all of them).
points no longer means the most wanted class, student can indicate that, for instance, all of the classes are equally desired (by giving the same amount of points to all of them).
We can consider this approach even further, by dividing student’s points by the total possible amount of points which the student can gain in just one course. As with the previous method, this is a matter of particular needs.
Summary
Today we described a very simple method of calculating happiness. In next parts we will consider more requirements which will greatly enhance our cost function.