This is the tenth part of the ILP series. For your convenience you can find other parts in the table of contents in Part 1 – Boolean algebra
Today we are going to use conditional operator to implement something similar to selection sort. Let’s begin.
Table of Contents
Algorithm
Selection sort goes as follows:
|
1 2 3 |
for i from 0 to array.length find minimum in array[i+1..array.length] swap found element with array[i] |
In every iteration we look for the lowest element in the rest of the array and then we swap current element with the one we have just found. We are going to implement something similar. Because we don’t know yet how to define loop, we need to define order in different way. Basically, we will define requirements for element on every single position which will make sure that the array is sorted.
Variables
We will start with the following variables:
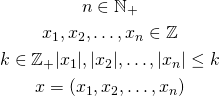
We have a vector of ![]() integer variables. We are going to compare values so we need to add constraints for maximum possible value for every variable.
integer variables. We are going to compare values so we need to add constraints for maximum possible value for every variable.
We need another vector which will represent the sorted variables:
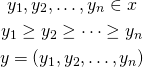
![]() is just a sorted vector
is just a sorted vector ![]() . Before we define the general formula, let us start with an example.
. Before we define the general formula, let us start with an example.
Sorting three variables
Imagine that we want to sort three variables ![]() . For now let’s also assume that we have no duplicates, so
. For now let’s also assume that we have no duplicates, so ![]() .
.
First, we need to compare every pair and check the ordering. We calculate the following variables:
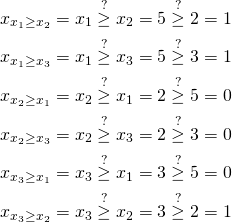
We have compared all pairs and for each variable we know the number of smaller variables. Now we need to know the total count of not less variables:
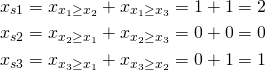
We are almost there. We have compared the values and we know their ordering. Now we need to construct final vector. Value ![]() is the i-th biggest value:
is the i-th biggest value:
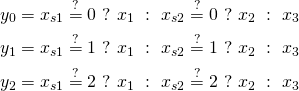
For every ![]() we choose variable which is not less than
we choose variable which is not less than ![]() different values. We assumed that all
different values. We assumed that all ![]() are different so there is only one value which satisfies the condition. However, if that is not be the case we might modify the formula to handle the duplicates:
are different so there is only one value which satisfies the condition. However, if that is not be the case we might modify the formula to handle the duplicates:
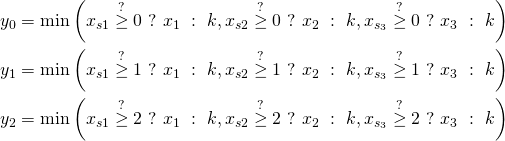
For every ![]() we choose select values which are not less than at least
we choose select values which are not less than at least ![]() different values and then we choose the minimum. For instance, when
different values and then we choose the minimum. For instance, when ![]() , every
, every ![]() is one, so the sums
is one, so the sums ![]() are equal to
are equal to ![]() , but we are still able to construct the final vector.
, but we are still able to construct the final vector.
Final formula
General sorting formula goes as follows:
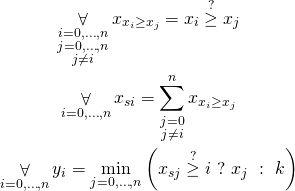
Summary
We are now able to sort any integer variables. This algorithm requires ![]() temporary variables because we compare every possible pair so is rather memory-consuming but works quite well and solvers are able to calculate the results rather smoothly.
temporary variables because we compare every possible pair so is rather memory-consuming but works quite well and solvers are able to calculate the results rather smoothly.
Bonus chatter
As an exercise you might want to implement counting sort. What is the space complexity of your solution?