ILP Part 58 – Kantoriiroodo

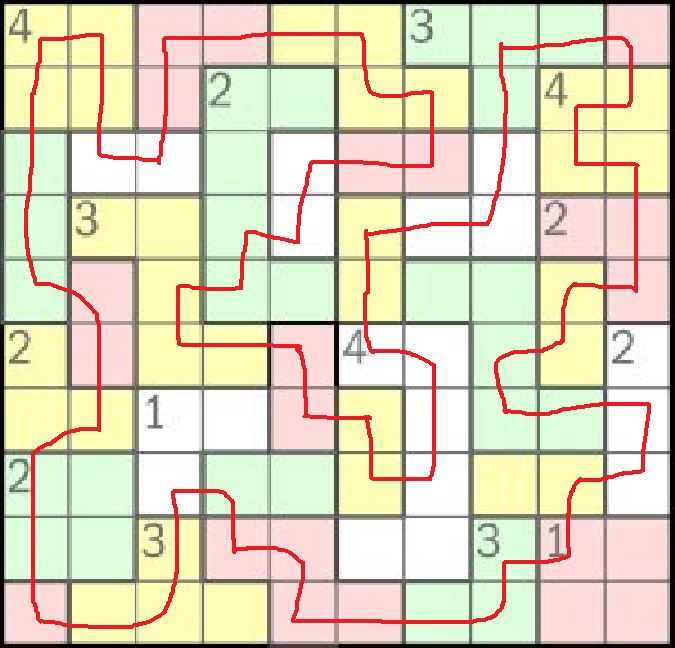
This is the fifty eighth part of the ILP series. For your convenience you can find other parts in the table of contents in Part 1 – Boolean algebra

Today we are going to solve kantoriiroodo riddle. Refer to the link to see how it works. Basically, we have a board of any size (like a chess board) divided into multiple “parcels” just like building parcels. Each parcel may (but is not obliged to) have a cost. We want to build a closed road (basically a loop) which goes through multiple fields and satisfies the following:

• It can enter and exit the parcel exactly once
• It must not cross itself
• It can go horizontally or vertically (so we cannot go diagonally, only four basic directions)
• Two neighboring fields may be empty in the solution if and only if they belong to the same parcel
• If parcel has a cost then it indicates how many fields of the parcel need to be occupied by road (no more, no less)

Let’s solve it with ILP. For each field we will have four variables indicating whether we have a road going up, down, left, or right. Full solution looks like this:

In lines 1-12 we specify the parcels. The example is from the linked blog (the second example, without given solution). You can see each character denotes parcel owner.

In lines 14-29 we specify how many fields we need to take for the road for each parcel with a cost. Notice that some parcels do not have a cost.

First, in lines 38-60 we initialize variables for each directions. Not all variables exist as we can go out of the board. Each variable is a binary integer denoting whether given direction is used for the road or not. Also, we make sure that if we go up from some field then we at the same time go down from the field above (and the same for other directions).

Lines 62-72 specify that we use each field exactly once – the road doesn’t cross itself. For that we must have either zero directions used in the field (meaning there is no road in the field) or exactly two directions.

In lines 76-96 we make sure neighboring fields of different parcels are not empty. We iterate through fields and check if they have same owners – if they don’t then we add directions for both of them and make sure they are not zero (so there will be road in at least one of the fields).

In lines 98-114 we take the cost into account. For each parcel with a cost we find its fields, for each field we calculate a binary indicating whether there is a road or not (by using disjunction), finally we add all these results and make sure correct number of fields is used.

In lines 118-144 we make sure we enter and exit the parcel exactly once. For each field of the parcel we find its outer directions, add all of them and make sure there is one entrance and one exit.

Finally, we add a dummy goal and that’s all.

You may notice we didn’t specify the requirement that the road is a loop. This doesn’t break the solution but in general should be added as well. This can’t be added as a local requirement for each neighboring fields, should be considered globally and hence is slightly more sophisticated.

Result:

And the image: