ILP Part 105 — Sudoku Cube

~ afish

This is the one hundred and fifth part of the ILP series. For your convenience you can find other parts in the table of contents in Part 1 – Boolean algebra

Today we are going to solve the Sudoku Cube. It’s a variation of the regular Rubik’s cube in which we have digits on the cube and each side must have exactly nine different digits from one to nine. What’s more, digits on a side must all look the same direction.

I took photos of my cube. You can see them below:

The tricky part is what to do. With the regular cube it’s rather clear where each piece should go. The hard part is figuring out how to put it into place. With Sudoku Cube it’s much harder. We don’t actually see where to put each element. The first step is to “solve the grid”. We need to understand where to put elements.

Solving the grid

First, notice that the number 1 is symmetrical. We don’t know whether it’s facing “up” or “down”. Therefore, we need to assume it can look both directions. We could actually wonder similarly for number eight (which side is “up”) or six/nine, but for them we can make some assumptions. Eight should be narrower at the top. Nine has a label on it.

Second, we don’t know which directions the sides look into. Also, it may not be obvious from the very beginning, but each center has an orientation. This is different from the regular cube. There are algorithms to do so and we’ll see them later. However, for now we need to assume that any side can look any direction. Sometimes the cube is convenient and the “middle strap” sides look upwards, but we can’t assume that.

Therefore, we need to figure out where pieces go. Once we have that, we can then solve the grid.

We start by defining the permutations in this way:

This looks cryptic, so let’s analyze step by step.

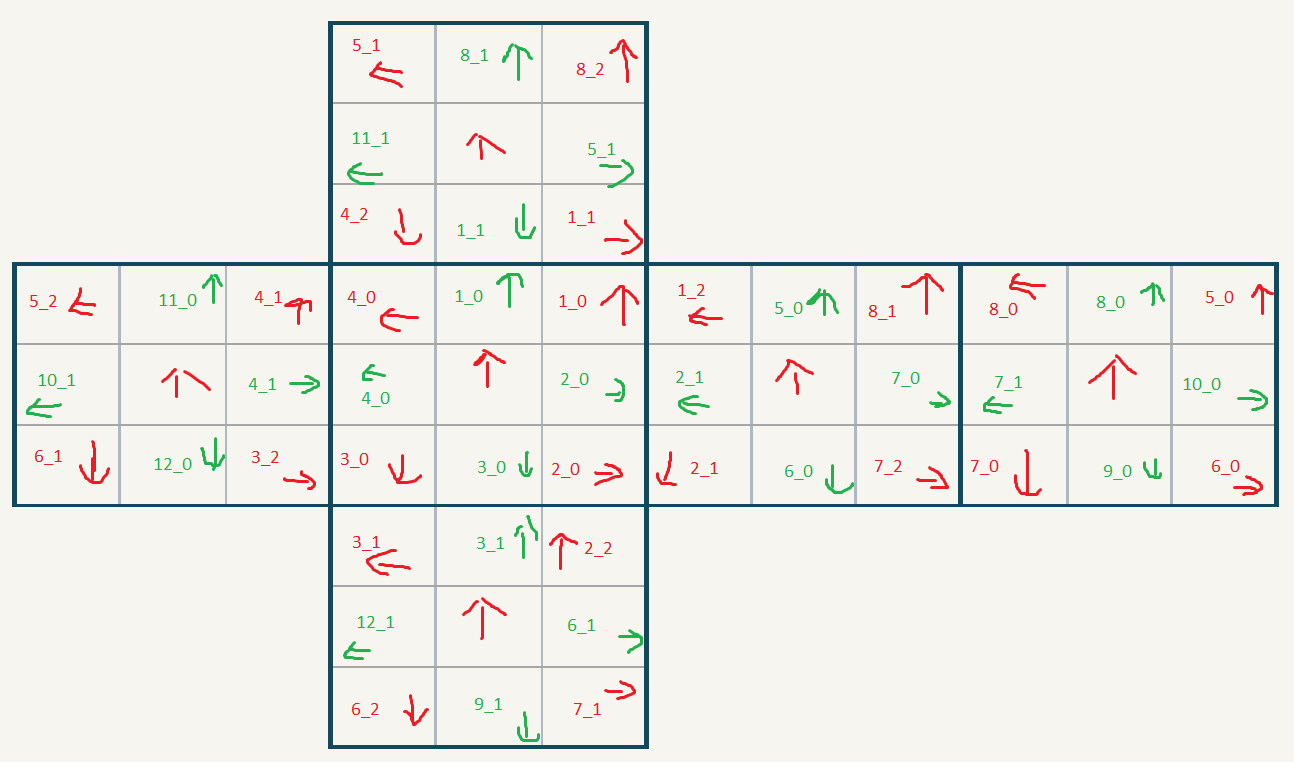
Let’s start with the corners marked with red arrows and numbers. We can see six faces of the cube. Going from left to right, top to bottom, the faces are: up, left, front, right, back, down. We have eight corners of the cube. Therefore, there are eight pieces that we can rotate and put in given places. Places are numbered from oen to eight, and permutations are numbered from zero to two. We are going to encode each piece as a list of numbers and list of rotations.

Let’s take the Picture from the above in which you can see free sides of the cube. Let’s say that the side with numbers 3, 9, 4, 6, 1, 5, 5, 7, 9 is the front side, and the side with numbers 5, 4, 6, 3, 6, 5, 8, 2, 2 is the top one. You can see that we have a corner with number 4 to the right of 9 and above 5. This is the corner that we marked as 1_0 on the diagram screen. So we can see, that we can encode this corner as having one with the following sequence of numbers: 4, 8, 4. Therefore 1_0 = 4, 1_1 = 8, 1_2 = 4.

You can see the arrow going up. This is an arbitrary indication which face I consider “upwards” of this given field. Similarly, for other fields. We want to encode the rotation of a piece based on the orientation of the digit. We have four directions: aligned with the arrow encoded as zero, rotated clockwise once by ninety degrees encoded as one, rotated twice encoded as two, rotated three times encoded as three. Therefore, the rotations of the numbers 4, 8, 4 are 3, 2, 1.

We can now take each corner and encode it properly. This should be the encoding:

We can do the same for edges (middles on the sides). We have twelve edges, each edge has two pieces. They are marked with green numbers and arrows. This is how we encode the cube:

We also have centers. We don’t care about their orientation at this point.

Formulas

We basically want to do the following:

  • For each corner: assign exactly one position to a corner (position from one to eight) and one permutation (from zero to two)
  • Do the same for edges (twelve positions and two permutations)
  • Make sure that each face has all pieces but center oriented the same way
  • Make sure that number one can be oriented upside down (as it looks the same)
  • Make sure each face has digits from one to nine

Sounds easy. Let’s see the first implementation.

First implementation

Let’s start by encoding the grid. First, we’d like to encode the positions from the chart above. For corners, we take the value like 4_1 and serialize it to one number as 4 * 3 + 1 = 13. We do similarly for edges:

Now, we encode the orientation of each field (arrows). We assume -1 means empty field:

Now, let’s make sure that each piece is put in a different position:

Let’s now start the magic. The idea is as follows: we ask the solver to assign positions and rotations to the pieces. We then iterate over all possibilities, check if a given possibility was selected by the solver, and then calculate the outcome. We then add the requirements to make the grid solved. Let’s begin with the corners.

For each corner from the diagram, we deserialize its position and permutation (lines 2-4). Next, we need to prepare some variables (lines 6-10) and then decipher the solution.

We iterate over each possible piece (line 12) and see if the corner was assigned to the field we analyze now (line 13). If that’s the case, then we copy the value of the assigned permutation to the temporary variable (lines 15-18).

Next, we do some magic. We would like to check all possible permutations to see which one was selected. To do that, we need to calculate what we call here finalPermutation. However, this is some kind of a cyclic dependency. First, we copy the permutation assigned by the solver and called corner.FinalPermutation to the variable piecePermutation (lines 15-18). Next, we need to add the permutation of the field to that value, calculate the modulo three, and assign that to the variable finalPermutation (lines 35-41). However, we then (or technically earlier) use the variable finalPermutation in line 21 to answer whether the current permutation we analyze is the one that was selected. Once we have that, we can copy the rotation of the corner (lines 23-26) and the value of the corner (lines 28-32).

Next, we do another time travel and we calculate the final orientation of the field by adding the orientation of the corner and the orientation (direction of the arrow) of the field. That’s in lines 43-49.

Finally, we return both the value and the final orientation (line 51).

Okay, we can now iterate over all corners of a given face:

We need to do a very similar code with the edges:

We iterate over all edges of a face:

And we also get the value of the center:

We can now setup a single face:

We take all the values and rotations of corners and edges (line 2). We then need to take all the ones and calculate additional rotation. We check if the value is one (line 6) and if that’s the case, then we add another rotation (upside-down), otherwise we return the same rotation (lines 7-8).

Finally, we take all the sides and make sure that they all have the same rotations. So for each pair of pieces, either their rotations are equal, or their rotation and alternative rotation are equal, or their alternative rotations are equal (lines 15-25).

Finally, we add the center (line 27) and make sure that all numbers are different (line 30) which means that we have the sudoku requirement met.

We can now configure all faces:

Let’s now add the goal, solve the problem, and print the result:

This works. In theory. I tried running that with NEOS for eight hours and it didn’t solve the problem, unfortunately. It was simply too complex.

Let’s see another solution.

Second implementation

In this solution we’ll apply many optimizations. We’ll store the positions as bitmasks instead of integers to use boolean flags (which are much faster). We won’t calculate the obtained direction of the face, but we’ll enforce which face must be selected. Finally, we won’t check the options and see if they were selected, but rather we will calculate what was selected end enforce the options. Let’s start.

First, we create a bitmask for directions of each face. We have six faces (sides) and four directions for each:

Next, we encode a bitmask what value was assigned to each corner side. We have six faces, four corners for each face, and nine numbers to choose from:

We do the similar for edges:

Now, we can use these bitmasks to constrain the solution. We make sure that digits on a face look all the same direction. So, for each face we take the direction flags and make sure that only one flag is selected:

We then make sure each corner has exactly one number. We have six faces and four corners on each face:

We now need to see how corners are stored. Previously, corner.FinalPosition was an integer. Now it’s a long bitmasks of positions and permutations. We have eight possible positions and three permutations:

Next, we make sure that each corner piece has exactly one position and one rotation selected:

Next we need to make sure that each corner of the cube has exactly one piece assigned. We have eight corners, for each corner we take bit flags of each piece, and make sure that only one was selected:

We do the same for edges:

Now we need to make sure that each side has sudoku numbers:

We need two additional mappings from corners and edges to faces:

We also need to know where each corner is (whether it’s right top, right bottom, left bottom, left top). Similarly for edges (top, right, bottom, left):

With all that prepared we can finally assert the corners:

We take some metadata about the piece we are in (lines 2-6). Next, we iterate over all corners and permutations. However, this time instead of asking “is this corner in that permutation assigned to this field”, we simply take what was assigned and enforce the proper bitflags.

We first take the bit indicating whether a given piece was assigned to this corner and this permutation (line 10). Next, we calculate the final permutation in this field (line 11) and the final rotation including directions of the arrows (line 12). We also take the value of the piece (line 13). Notice that this time we don’t extract these values from the ILP variables. We precalculate them outside of the model which is much faster.

We can now do two simple constraints. First, if this digit is one (line 15) then we enforce this constraint: if this piece was picked (line 17), then direction of the face needs to be either the same as the direction of the piece (line 19) or the opposite (line 20). If the digit is not one, then we enforce the constraint, that if the piece was picked, than the boolean flag indicating the direction of the face must be selected (line 26).

The crucial difference is that we don’t calculate the direction within the model now. We do the causation outside of the model. We encode something like “I don’t know what piece was selected, but if the piece I’m currently looking at was selected, then this bit flag of the face direction must be selected too”.

The next constraint we add is for the numbers: if the piece was picked (line 31) then the number assigned to the corner is selected (line 32). Again, we don’t care about the actual value if it was selected or not. We just make sure that if it was selected, then some other bit flag is set.

We can now setup all corners:

We do very similar stuff for edges:

Finally, we encode faces:

We run it and this is the result we get:

It took 30 milliseconds to find the answer. First implementation couldn’t do that in 8 hours. Not to mention that the first implementation ran on Gurobi in NEOS, and the second one was running with CPLEX on my local machine.

Reading the solution

Let’s read the solution. We can see that when we hold the cube in a way that the top side has center 6, front side has center 1, and bottom side has center 1, then the top side looks to the left, left side looks down, front and right and back and down sides look to the right. We can also see all the numbers assigned, so we know the “colors” of the pieces. We can now apply the regular algorithms for solving the cube.

The last remaining piece is how to rotate centers. There are two algorithms for that:

  • Top center clockwise and front center counter-clockwise: f b’ l r’ u d’ f’ u’ d l’ r f’ b u
  • Top center 180 degrees: u r l uu r’ l’ u r l uu r’ l’

We can now easily solve the cube:

Lessons learned

There are some important tricks we applied to optimize the solution:

  1. We stored numbers as bitflags instead of storing them as integers. This is a common trick. If you know the range of the variables, then don’t use integers. Bitflags are much faster.
  2. We precalcualted results outside of the model. Instead of creating a variable with a value of the face rotation, we calculated the rotation outside of the model, and then added a constraint (basically, an “if” condition in the ILP)
  3. We didn’t compare numbers. Generally, don’t do that if it’s possible. Instead, just create a boolean flag indicating the result of comparison and use it later onw. The difference is subtle but improves the performance a lot.
  4. We didn’t use “if else” conditions. They look easy, but they are really the performance killer.

With all these improvements in place, we managed to solve the cube in milliseconds.