ILP Part 67 — Parcelacja

~ afish

This is the sixtieth seventh part of the ILP series. For your convenience you can find other parts in the table of contents in Part 1 – Boolean algebra

Today we are going to solve Parcelacja.

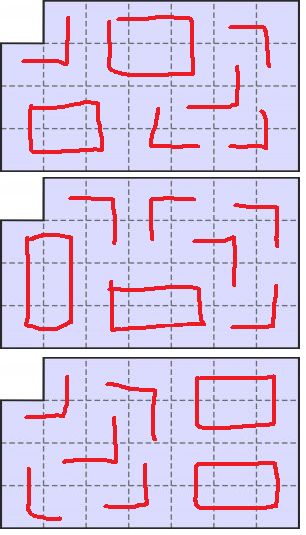
We have a rectangular board without top left corner. We need to put two 3×2 rectangles and 5 triminoes to fill the board. Additional constraint is: no two triminoes can make a 3×2 rectangle. Rotations are allowed.

Solution:

Let’s analyze the code. First, in lines 1-6 we define the board. Spaces represent missing fields, zeroes show allowed positions.

Next, in lines 8-38 we define shapes with rotations. Each two dimensional array of strings represent one “shape” with all rotations. We also specify number of expected pieces of given kind.

Next, in lines 40-50 we prepare solver and variables.

In lines 52-70 we define our model. Each field is represented by expando. Each dynamic object has 3 fields: PieceId for numbering pieces (and making sure they are continuous etc). PieceType for deciding which shape and rotation we use (we number them from 1). AllowedShapes is to ban invalid positions to start a shape. In line 66 we make sure we only use valid number of piece type. In line 68 we make sure that if a field starts a shape then its PieceId is equal to the position on the board (so we uniquely identify each field).

Next, we define shapes. In lines 72-122 we do the magic. We iterate over each field. Next, for each field we iterate over each shape. We check every part of the shape and check if it’s non-empty (line 86). Next, we check if we didn’t jump out of the board (line 87), if there is a field over there (line 92). For each shape we define a “designatedField” being first non-empty part of the shape. So in line 98 we check if we already found a designated field and otherwise we set it. Next, in line 103 we store field for this shape’s part.

Next, in lines 107-119 we are sure that current shape can fit on the board and that we have a designated part. So we remember that designated part can hold this shape (line 108) and then in lines 110-117 we encode the constraint that all parts for the shape must have PieceId equal to the designated part if we decide to use the shape here.

Next, in lines 124-140 we prohibit invalid shapes (invalid as they don’t fit on the board in given position). We iterate over all fields, check if given field can be a designated point for given shape, and if not then we explicitly mark it as banned.

In lines 142-159 we count shapes and make sure we meet constraints (2 rectangles and 5 triminoes).

Finally, in lines 161-204 we ban triminoes from forming rectangles. In lines 161-175 we ban horizontal rectangle, then in line 177-190 we ban one type of vertical rectangle and then the another in lines 192-204.

Next, we add the goal in line 206. Next, in lines 208-209 we populate the solution pool (to find all solutions). Finally, we print them out. First part prints ids (so you can see how pieces were placed) and then we print the designated parts determining the type.

That’s it. The output:

You can see it found 3 solutions, presented below:

Solutions