This is the twenty second part of the ILP series. For your convenience you can find other parts in the table of contents in Part 1 – Boolean algebra
Last time we saw how to include preferences points in the cost function. Today we are going to implement yet another nice feature of our scheduling system — we are going to include continuous classes in the cost function.
Introduction
By including only preferences points we try to maximize the students happiness based on their choices. However, the solver doesn’t consider any other requirements which might be very helpful when a student does not get exactly what he or she wants. For instance, when someone is assigned to two classes with a gap between them, he or she needs to waste some time waiting for the second class. It is very annoying for people who are not able to return home in such a short period of time.
There is also another case for continuous classes. Some students do not care which classes they get and all they would like is to have a continuous schedule, which means that their classes occur one after another. It is so because students are working and they prefer to study in the evenings, or they live far away from the university and they need to travel by bus for a few hours every day. In this case having one class, then one hour break, and another class is inconvenient, because such a student cannot go home and rest or go to work.
Implementation
Let us assume that we have a list of pairs of co-occurring classes. By “co-occurring” we mean situation, when one class starts right after another one ends. For each pair of such classes and for each student we create a boolean variable indicating whether the student is assigned to both of the classes. We define the following variables:

When variable ![]() is equal to one, the student is assigned to two classes occurring one after another. We can now sum all these variables, multiply them by coefficient
is equal to one, the student is assigned to two classes occurring one after another. We can now sum all these variables, multiply them by coefficient ![]() (whose meaning is analogous to the coefficient
(whose meaning is analogous to the coefficient ![]() described in the previous section), and add to the cost function:
described in the previous section), and add to the cost function:
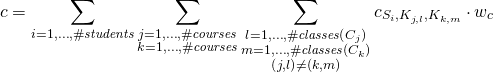
By changing the value of ![]() , we can change the behaviour of the solver — whether we prefer the more continuous schedules or schedules more going on with students’ preference points.
, we can change the behaviour of the solver — whether we prefer the more continuous schedules or schedules more going on with students’ preference points.
Summary
It is rather an easy task to include continuous classes in the cost function, however, it is very powerful. Next time we are going to do something similar: we are going to maximize the number of days off for students.